题目内容
【题目】如图，四棱锥PABCD中，侧面PAD是正三角形，底面ABCD是菱形，且∠ABC＝60°，M为PC的中点．
(1)求证：PC⊥AD.
(2)在棱PB上是否存在一点Q，使得A，Q，M，D四点共面？若存在，指出点Q的位置并证明；若不存在，请说明理由．
【答案】（1）见解析；（2）见解析
【解析】
（1）取AD的中点O，连接OP，OC，AC，由线面垂直判定定理证明AD⊥平面POC，继而得到PC⊥AD
（2）取棱PB的中点Q，连接QM，证明QM∥AD，从而A，Q，M，D四点共面
(1)证明：如图，取AD的中点O，连接OP，OC，AC.
依题意可知△PAD，△ACD均为正三角形．
所以OC⊥AD，OP⊥AD.
又OC∩OP＝O，OC平面POC，OP平面POC，所以AD⊥平面POC.
又PC平面POC，所以PC⊥AD.
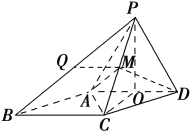
(2)解：当点Q为棱PB的中点时，A，Q，M，D四点共面．
证明如下：
取棱PB的中点Q，连接QM.
因为M为PC的中点，所以QM∥BC.
在菱形ABCD中，AD∥BC，所以QM∥AD.
所以A，Q，M，D四点共面．
练习册系列答案
阅读快车系列答案
相关题目
