题目内容
【题目】设函数![]() 的定义域为
的定义域为![]() ,
, ![]() , 当
, 当![]() 时,
时,![]() , 则函数
, 则函数![]() 在区间
在区间![]() 上的所有零点的和为( )
上的所有零点的和为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
根据f(x)的对称性和奇偶性可知f(x)在[﹣![]() ,
,![]() ]上共有3条对称轴,x=0,x=1,x=2,根据三角函数的对称性可知y=|cos(πx)|也关于x=0,x=1,x=2对称,故而g(x)在[﹣
]上共有3条对称轴,x=0,x=1,x=2,根据三角函数的对称性可知y=|cos(πx)|也关于x=0,x=1,x=2对称,故而g(x)在[﹣![]() ,
,![]() ]上3条对称轴,根据f(x)和y=|cos(πx)|在[0,1]上的函数图象,判断g(x)在[﹣
]上3条对称轴,根据f(x)和y=|cos(πx)|在[0,1]上的函数图象,判断g(x)在[﹣![]() ,
,![]() ]上的零点分布情况,利用函数的对称性得出零点之和.
]上的零点分布情况,利用函数的对称性得出零点之和.
∵f(x)=f(2﹣x),∴f(x)关于x=1对称,
∵f(﹣x)=f(x),∴f(x)根与x=0对称,
∵f(x)=f(2﹣x)=f(x﹣2),∴f(x)=f(x+2),
∴f(x)是以2为周期的函数,
∴f(x)在[﹣![]() ,
,![]() ]上共有3条对称轴,分别为x=0,x=1,x=2,
]上共有3条对称轴,分别为x=0,x=1,x=2,
又y=|cos(πx)关于x=0,x=1,x=2对称,
∴x=0,x=1,x=2为g(x)的对称轴.
作出y=|cos(πx)|和y=x3在[0,1]上的函数图象如图所示:
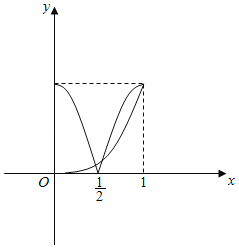
由图象可知g(x)在(0,![]() )和(
)和(![]() ,1)上各有1个零点.
,1)上各有1个零点.
又g(1)=0,∴g(x)在[﹣![]() ,
,![]() ]上共有7个零点,
]上共有7个零点,
设这7个零点从小到大依次为x1,x2,x3,…x6,x7.
则x1,x2关于x=0对称,x3,x5关于x=1对称,x4=1,x6,x7关于x=2对称.
∴x1+x2=0,x3+x5=2,x6+x7=4,
∴x1+x2+x3+x4+x5+x6+x7=7.
故选:A.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目