Question

【题目】在锐角三角形ABC中，若，且满足关系式，则a+c的取值范围是（ ）

A.B.C.D.

Answer 1

【答案】A

【解析】

由cosBsinB＝2，可得B＝60°，由，推导出b，再由余弦定理可得3ac＝（a+c）2﹣3，由此能求出a+c的取值范围．

∵在锐角△ABC中，A、B、C分别为△ABC三边a，b，c所对的角．

，

∴2sin（B+30°）＝2，

∴B＝60°，

∵，

∴，

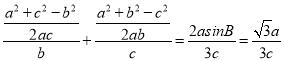解得b，

∴a+c．

由余弦定理b2＝a2+c2﹣2accosB，

即（）2＝a2+c2﹣2accos60°，

即3＝（a+c）2﹣2ac﹣2ac，即3＝（a+c）2﹣3ac，

即3ac＝（a+c）2﹣3，即[（a+c）2﹣3]＝3ac≤3[（a+c）]2，

令t＝a+c，

即t2﹣3＝3ac≤3（ ）2，整理得t2≤12，

即t的最大值2即a+c的最大值为2，

综上，a+c的取值范围是（，2]．

故选：A．