Question

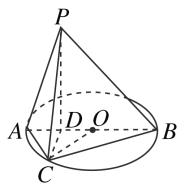
【题目】如图所示，已知AB为圆O的直径，且AB＝4，点D为线段AB上一点，且，点C为圆O上一点，且.点P在圆O所在平面上的正投影为点D，PD＝DB.

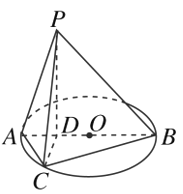
(1)求证：CD⊥平面PAB；

(2)求直线PC与平面PAB所成的角．

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）连接CO，由题意可得△ACO为等边三角形，即得CD⊥AO，再由题意得PD⊥CD，即证得CD⊥平面PAB

（2）由(1)知∠CPD是直线PC与平面PAB所成的角，在三角形中结合各边长解三角形即可求出结果

(1)证明：连接CO，

由3AD＝DB知，点D为AO的中点．

又因为AB为圆O的直径，所以AC⊥CB.

由AC＝BC知，∠CAB＝60°，

所以△ACO为等边三角形．故CD⊥AO.

因为点P在圆O所在平面上的正投影为点D，

所以PD⊥平面ABC，又CD平面ABC，所以PD⊥CD，

由PD平面PAB，AO平面PAB，且PD∩AO＝D，

得CD⊥平面PAB.

(2)由(1)知∠CPD是直线PC与平面PAB所成的角，

又△AOC是边长为2的正三角形，所以CD＝.

在Rt△PCD中，PD＝DB＝3，CD＝，

所以，∠CPD＝30°，

即直线PC与平面PAB所成的角为30°.