题目内容
已知定义在R上的函数y = f(x)满足下列三个条件:①对任意的x∈R都有f(x+2)=" -" f(x);②对于任意的0≤x1<x2≤2,都有f(x1)<f(x2),③y=f(x+2)的图象关于y轴对称,则下列结论中正确的是( )
| A.f(4.5)<f(6.5)<f(7) | B.f(4.5)<f(7)<f(6.5) |
| C.f(7)<f(4.5)<f(6.5) | D.f(7)<f(6.5)<f(4.5) |
B
解析试题分析:求解本题需要先把函数的性质研究清楚,由三个条件知函数周期为4,其对称轴方程为x=2,在区间[0,2]上是增函数,观察四个选项发现自变量都不在已知的单调区间内故应用相关的性质将其值用区间[0,2]上的函数值表示出,以方便利用单调性比较大小.
由①②③三个条件知函数的周期是4,在区间[0,2]上是增函数且其对称轴为x=2∴f(4.5)=f(0.5),f(7)=f(3)=f(2+1)=f(2-1)=f(1),f(6.5)f(2.5)=f(2+0.5)=f(2-0.5)=f(1.5)∵0<0.5<1<1.5<2,函数y=f(x)在区间[0,2]上是增函数∴f(0.5)<f(1)<f(1.5),即f(4.5)<f(7)<f(6.5)
故选B.
考点:本试题主要考查了是函数单调性的应用,综合考查了函数的周期性,函数的对称性与函数的单调性,以及函数图象的平移规律,涉及到了函数的三个主要性质,本题中同期性与对称性的作用是将不在同一个单调区间上的函数值的大小比较问题转化成一个单调区间上来比较,函数图象关于直线x=a对称,有两个等价方程一为f(a+x)=f(a-x),一为f(x)=f(2a-x),做题时应根据题目条件灵活选择对称性的表达形式.
点评:解决该试题的关键将不在同一个单调区间上的函数值的大小比较问题转化成一个单调区间上来比较。

设函数 上单调递增,则
上单调递增,则 的大小关系为( )
的大小关系为( )
A. | B. |
C. | D.不确定 |
下列各组表示同一函数的是( )
A.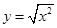 与 与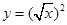 | B.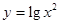 与 与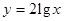 |
C.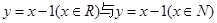 | D.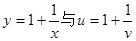 |
偶函数 在区间
在区间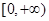 单调增加,则满足
单调增加,则满足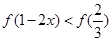 的
的 取值范围是( )
取值范围是( )
A.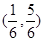 | B.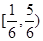 | C.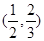 | D. |
若函数y=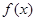 的图象经过(0,-1),则y=
的图象经过(0,-1),则y=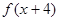 的反函数图象经过点( )
的反函数图象经过点( )
| A.(4,一1) | B.(一1,-4) | C.(-4,- 1) | D.(1,-4) |
如果两个函数的对应关系相同,值域相同,但定义域不同,则这两个函数为“同族函数”,那么函数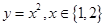 的“同族函数”有( )
的“同族函数”有( )
| A.3个 | B.7个 | C.8个 | D.9个 |
已知函数 是定义在
是定义在 上的奇函数,且
上的奇函数,且 是偶函数,当
是偶函数,当 时,
时, ,则
,则 =【 】
=【 】
| A.8 | B.- | C. | D.-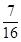 |
设奇函数 在
在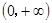 上为增函数,且
上为增函数,且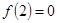 ,则不等式
,则不等式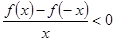 解集为( )
解集为( )
A.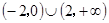 | B.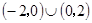 | C.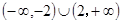 | D.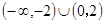 |
若 ,定义:
,定义: ,例如
,例如 ,则函数
,则函数
| A.是偶函数 | B.是奇函数 |
| C.既是奇函数也是偶函数 | D.既不是奇函数也不是偶函数 |