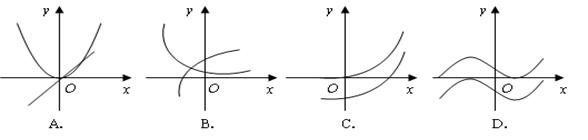
题目内容
设函数 上单调递增,则
上单调递增,则 的大小关系为( )
的大小关系为( )
A. | B. |
C. | D.不确定 |
B
解析试题分析:因为f(-x)=f(x),所以f(x)为偶函数,又因为f(x)在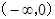 上单调递增,所以f(x)在
上单调递增,所以f(x)在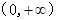 上单调递减,所以0<a<1,所以0<a+1<2,所以f(a+1)>f(2).故选B.
上单调递减,所以0<a<1,所以0<a+1<2,所以f(a+1)>f(2).故选B.
考点:函数的奇偶性与单调性.
点评:如果一个函数是奇函数,那么它在关于原点的对称区间上具有相同的单调性,如果一个函数是偶函数,它在关于原点的对称区间上具有相反的单调性.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
已知函数 的图象如图所示,则
的图象如图所示,则 满足的关系是( )
满足的关系是( )
A. | B.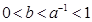 |
C. | D. |
已知函数 ,则
,则 是( )
是( )
| A.奇函数 | B.偶函数 |
| C.既是奇函数又是偶函数 | D.非奇函数非偶函数 |
 为定义在
为定义在 上的偶函数,对任意的
上的偶函数,对任意的

 为增函数,则下列各式成立的是 ( )
为增函数,则下列各式成立的是 ( )
A. | B. |
C. | D. |
下列函数中是偶函数的是
A.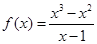 | B.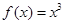 | C.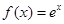 | D.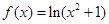 |
已知 其中
其中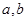 为常数,若
为常数,若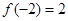 ,则
,则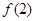 =( )
=( )
| A.2 | B.-6 | C.-10 | D.-4 |
若 为奇函数,在
为奇函数,在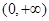 上单调递增,且
上单调递增,且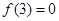 ,则
,则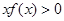 的解集为
的解集为
A.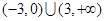 | B.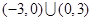 |
C.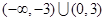 | D.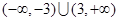 |
已知定义在R上的函数y = f(x)满足下列三个条件:①对任意的x∈R都有f(x+2)=" -" f(x);②对于任意的0≤x1<x2≤2,都有f(x1)<f(x2),③y=f(x+2)的图象关于y轴对称,则下列结论中正确的是( )
| A.f(4.5)<f(6.5)<f(7) | B.f(4.5)<f(7)<f(6.5) |
| C.f(7)<f(4.5)<f(6.5) | D.f(7)<f(6.5)<f(4.5) |
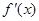 是函数
是函数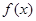 的导函数,将
的导函数,将 和
和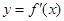 的图象画在同一个直角坐标系中,不可能正确的是( )
的图象画在同一个直角坐标系中,不可能正确的是( )