题目内容
若函数y=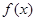 的图象经过(0,-1),则y=
的图象经过(0,-1),则y=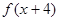 的反函数图象经过点( )
的反函数图象经过点( )
| A.(4,一1) | B.(一1,-4) | C.(-4,- 1) | D.(1,-4) |
B
解析试题分析:根据原函数与反函数图象之间的关系可得结论,对于原函数与复合函数的所过定点问题,本题可利用在函数值-1保持不变的情况下,求出与原函数自变量x=0与之对应的复合函数的自变量x=-4,由函数y=f(x)的图象经过点(0,-1),所以当x=-4时有f(4+x)=f(0)=-1,从而函数y=f(4+x)过点(-4,-1),则函数y=f(4+x)的反函数并经过点(-1,-4),故答案为B。
考点:本题主要考查复合函数与原函数关系,以及函数与反函数关系,属于基础题
点评:解决该试题的关键是原函数过点(a,b),其反函数必定过点(b,a)。

练习册系列答案
相关题目
 为定义在
为定义在 上的偶函数,对任意的
上的偶函数,对任意的

 为增函数,则下列各式成立的是 ( )
为增函数,则下列各式成立的是 ( )
A. | B. |
C. | D. |
某工厂今年前五个月每月生产某种产品的数量C(件)关于时间 (月)的函数图象如图所示,则这个工厂对这种产品来说( )
(月)的函数图象如图所示,则这个工厂对这种产品来说( )
| A.一至三月每月生产数量逐月增加,四、五两月每月生产数量逐月减少 |
| B.一至三月每月生产数量逐月增加,四、五月每月生产数量与三月持平 |
| C.一至三月每月生产数量逐月增加,四、五两月均停止生产 |
| D.一至三月每月生产数量不变,四、五两月均停止生产 |
函数 的零点所在的区间是( )
的零点所在的区间是( )
A. | B. | C. | D. |
设函数 ,则有( )
,则有( )
A. 是奇函数, 是奇函数, | B. 是奇函数, 是奇函数, |
C. 是偶函数 是偶函数 | D. 是偶函数, 是偶函数, |
已知定义在R上的函数y = f(x)满足下列三个条件:①对任意的x∈R都有f(x+2)=" -" f(x);②对于任意的0≤x1<x2≤2,都有f(x1)<f(x2),③y=f(x+2)的图象关于y轴对称,则下列结论中正确的是( )
| A.f(4.5)<f(6.5)<f(7) | B.f(4.5)<f(7)<f(6.5) |
| C.f(7)<f(4.5)<f(6.5) | D.f(7)<f(6.5)<f(4.5) |
已知函数 定义域为
定义域为 ,则
,则 的定义域为( )
的定义域为( )
A. | B. | C. | D. |
已知 为实数,且
为实数,且 则
则 的值是:
的值是:
| A.-3 | B.3 | C.-1 | D.1 |
