题目内容
16．已知x1，x2是函数f（x）=$\frac{1}{3}$x3+$\frac{1}{2}$ax2+2bx+c（a，b，c∈R）的两个极值，x1∈（-2，0），x2∈（0，2），则2a+b的取值范围为（ ）| A． | （-∞，-2） | B． | （-2，4） | C． | （-2，+∞） | D． | （-4，4） |
分析 求导函数，利用f（x）的两个极值点分别是x1，x2，x1∈（-2，0），x2∈（0，2），建立不等式，利用平面区域，即可求2a+b的取值范围．
解答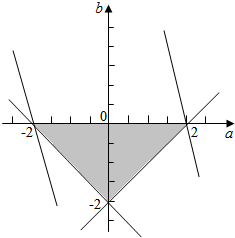 
解：由题意，f′（x）=x2+ax+2b．
∵f（x）的两个极值点分别是x1，x2，x1∈（-2，0），x2∈（0，2）
∴$\left\{\begin{array}{l}{f′（-2）=4-2a+2b＞0}\\{f′（0）=2b＜0}\\{f′（2）=4+2a+2b＞0}\end{array}\right.$，
对应的平面区域如图所示：
令z=2a+b，则b=-2a+z，
由图象得：直线b=-2a+z过（-2，0）时，z最小，最小值是-4，
在（2，0）处，z=2a+b最大，最大值是4，
∴2a+b的取值范围是（-4，4）．
故选：D．
点评 本题考查导数知识的运用，考查平面区域的运用，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
11．已知椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），过原点任作一条不与x轴重合的直线与椭圆交于A、B两点，若x轴上存在点C使得kCA•kCB=-$\frac{1}{2}$恒成立，则椭圆的离心率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | $\frac{1}{3}$ |
1．若等差数列{an}满足a12+a32=2，则$\frac{{{a}_{3}}^{2}+{{a}_{4}}^{2}}{{{a}_{4}}^{2}+{{a}_{5}}^{2}}$的取值范围是（ ）
| A． | [1，3] | B． | [$\sqrt{5}$-1，$\sqrt{5}$十1] | C． | [3-2$\sqrt{2}$，3+2$\sqrt{2}$] | D． | [4-2$\sqrt{3}$，4+2$\sqrt{3}$]． |