题目内容
6．定义在R上的函数f（x）=ex+x2+sinx，则曲线y=f（x）在点（0，f（0））处的切线方程是2x-y+1=0．分析 求出原函数的导函数，得到函数在x=0处的导数，再求出切点坐标，代入直线方程的点斜式得答案．
解答 解：由f（x）=ex+x2+sinx，得
f′（x）=ex+2x+cosx，
∴f′（0）=e0+2×0+cos0=2，
又f（0）=e0+02+sin0=1，
∴曲线y=f（x）在点（0，f（0））处的切线方程是y=2x+1，即2x-y+1=0．
故答案为：2x-y+1=0．
点评 本题考查利用导数研究过曲线上某点处的切线方程，过曲线上某点处的切线的斜率，就是函数在该点处的导数值，是中档题．
练习册系列答案
相关题目
16．
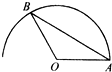如图所示，OA=1，在以O为圆心，OA为半径的半圆弧长任取一点B，则使△AOB的面积大于等于$\frac{1}{4}$的概率为（ ）
如图所示，OA=1，在以O为圆心，OA为半径的半圆弧长任取一点B，则使△AOB的面积大于等于$\frac{1}{4}$的概率为（ ）| A． | $\frac{2}{3}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{2}$ |
18．一个正方体的八个顶点都在同一个球面上，已知这个正方体的体积是8，则这个球的表面积是（ ）
| A． | 4π | B． | 8π | C． | 12π | D． | 24π |
16．已知x1，x2是函数f（x）=$\frac{1}{3}$x3+$\frac{1}{2}$ax2+2bx+c（a，b，c∈R）的两个极值，x1∈（-2，0），x2∈（0，2），则2a+b的取值范围为（ ）
| A． | （-∞，-2） | B． | （-2，4） | C． | （-2，+∞） | D． | （-4，4） |