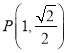题目内容
【题目】已知函数![]() ,
, ![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,判断方程
时,判断方程![]() 在区间
在区间![]() 上有无实根;
上有无实根;
(3)若![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ;(2) 内无实数根;(3)
;(2) 内无实数根;(3)![]() .
.
【解析】试题分析:(2)把m的值代入后,求出f(1),求出x=1时函数的导数,由点斜式写出曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)代入m的值,把判断方程f(x)=g(x)在区间(1,+∞)上有无实根转化为判断函数h(x)=f(x)﹣g(x)在(1,+∞)上有无零点问题,求导后利用函数的单调性即可得到答案;
(Ⅲ)把f(x)和g(x)的解析式代入不等式,整理变形后把参数m分离出来,x∈(1,e]时,不等式f(x)﹣g(x)<2恒成立,转化为实数m小于一个函数在(1,e]上的最小值,然后利用导数分析函数在(1,e]上的最小值.
试题解析:
(1)![]() 时,
时, ![]() ,
, ![]() ,
, ![]() ,切点坐标为
,切点坐标为![]() ,
,
∴切线方程为![]()
(2)![]() 时,令
时,令![]() ,
,
![]() ,∴
,∴![]() 在
在![]() 上为增函数,
上为增函数,
又![]() ,所以
,所以![]() 在
在![]() 内无实数根.
内无实数根.
(3)![]() 恒成立,即
恒成立,即![]() 恒成立.
恒成立.
又![]() ,则当
,则当![]() 时,
时, ![]() 恒成立,
恒成立,
令![]() ,只需
,只需![]() 小于
小于![]() 的最小值.
的最小值.
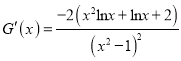 ,∵
,∵![]() ,∴
,∴![]() ,∴
,∴![]() 时,
时, ![]() ,
,
∴![]() 在
在![]() 上单调递减,∴
上单调递减,∴![]() 在
在![]() 的最小值为
的最小值为![]() ,
,
则![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目