题目内容
5.已知关于a的方程2x+1=a2+a有解,则实数a的取值范围是a>$\frac{-1+\sqrt{5}}{2}$或a<$\frac{-1-\sqrt{5}}{2}$.分析 根据函数和方程之间的关系转化为求函数y=2x+1的取值范围即可.
解答 解:∵y=2x+1>1,
∴若关于a的方程2x+1=a2+a有解,
则a2+a>1,
即a2+a-1>0,
解得a>$\frac{-1+\sqrt{5}}{2}$或a<$\frac{-1-\sqrt{5}}{2}$,
即实数a的取值范围是a>$\frac{-1+\sqrt{5}}{2}$或a<$\frac{-1-\sqrt{5}}{2}$,
故答案为:a>$\frac{-1+\sqrt{5}}{2}$或a<$\frac{-1-\sqrt{5}}{2}$
点评 本题主要考查函数与方程的应用,根据指数函数的性质是解决本题的关键.

练习册系列答案
相关题目
16.在侧棱长为2$\sqrt{3}$的正三棱锥S-ABC中,∠ASB=∠BSC=∠CSA=40°,过A作截面AMN,则截面的最小周长为( )
| A. | 2$\sqrt{2}$ | B. | 4 | C. | 6 | D. | 10 |
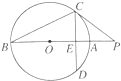 如图,PC切圆O于点C,割线PAB经过圆心O,弦CD⊥AB于点E,若圆O的半径为2,PA=1,求PC•CE的值.
如图,PC切圆O于点C,割线PAB经过圆心O,弦CD⊥AB于点E,若圆O的半径为2,PA=1,求PC•CE的值.