题目内容

2．求函数y=（log2x）2-4log2x+5（1≤x≤2）的值域．

分析 ：函数y=（log2x）2-4log2x+5=$（lo{g}_{2}x-2）^{2}$+1．由于1≤x≤2，可得0≤log2x≤1，利用二次函数的单调性即可得出．

解答 解：函数y=（log2x）2-4log2x+5
=$（lo{g}_{2}x-2）^{2}$+1
∵1≤x≤2，
∴0≤log2x≤1，
∴2≤y≤5．
∴函数的值域为[2，5]．

点评 本题考查了二次函数的单调性、对数函数的单调性，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
12．已知函数f（x）=3${\;}^{-{x}^{2}+ax+2}$．
（1）若函数f（x）为偶函数，求实数a的值；
（2）若a=2，求函数f（x）的单调区间，并求出其值域．
13．函数y=2${\;}^{{x}^{2}-2x-6}$的递减区间为（-∞，1）．
10．定义在R上的奇函数f（x），当x∈（0，+∞）时的解析式为f（x）=-x2+4x-3．
（1）求这个函数在R上的解析式；
（2）作出f（x）的图象，并根据图象直接写出函数f（x）的单调减区间．
17．R上的奇函数f（x）关于x=1对称，当x∈[0，1]时，f（x）=1-（x-1）2．
（1）证明f（x）为周期函数．
（2）求f（x）在x∈[-2，2]的表达式．
（3）结合图象在R上解关于x的方程f（x）=$\frac{x}{2}$．
1．函数f（x）=$\left\{\begin{array}{l}{（a-1）x+\frac{5}{2}，x≤1}\\{\frac{2a+1}{x}，x＞1}\end{array}\right.$，在定义域R上单调递减，则a的取值范围是（-$\frac{1}{2}$，$\frac{1}{2}$]．
8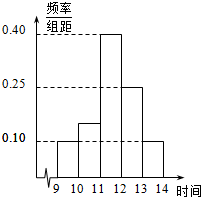．某商场在一日促销活动中，归该日9时到14时的销售额进行统计，其频率分布直方图如图所示，已知11时至12时的销售额为10万元，则10时到11时的销售额为（单位：万元）（　　）
A．2.5B．2.75C．3.25D．3.75
5．设a，b∈R，a+bi=$\frac{11-7i}{1-2i}$，则a+b的值为（　　）
A．8B．9C．10D．12
6．已知函数$f（x）=\sqrt{3}sinxcosx-{cos^2}x-\frac{1}{2}，x∈R$．
（ I）求$f（x）=-\frac{1}{2}$时x取值的集合；
（ II）已知△ABC内角A，B，C的对边分别为a，b，c，且c=3，f（C）=0，若向量$\overrightarrow m=（1，sinA）与\overrightarrow n=（2，sinB）$共线，求a，b的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网