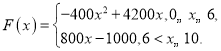题目内容
【题目】已知函数![]() (
(![]() 为自然对数的底数,
为自然对数的底数,![]() ).
).
(1)求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若对于任意![]() ,存在
,存在![]() ,使得
,使得![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)对函数![]() 求导,求得
求导,求得![]() ,
,![]() ,由直线的点斜式方程可求得切线;
,由直线的点斜式方程可求得切线;
(2)对函数![]() 求导,得出函数
求导,得出函数![]() 在
在![]() 上单调性,可求得函数
上单调性,可求得函数![]() 在
在![]() 上的最值,再根据对于任意
上的最值,再根据对于任意![]() ,存在
,存在![]() ,使得
,使得![]() ,则需
,则需![]() ,
,
讨论a可求得a的范围;
(3) )因为![]() ,所以由
,所以由![]() 得
得![]() 令
令![]() ,则
,则![]() ,分析导函数的正负,得出原函数的单调性,从而得出最值,根据不等式恒成立的思想得出求得a的范围.
,分析导函数的正负,得出原函数的单调性,从而得出最值,根据不等式恒成立的思想得出求得a的范围.
(1)![]() ,
,![]() ,
,![]() ,又
,又![]() ,
,
所以切线方程为:![]() ,即
,即![]() ;
;
(2)![]() ,
,![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,![]() ,
,
由于对于任意![]() ,存在
,存在![]() ,使得
,使得![]() ,则需
,则需![]() ,
,
![]()
当![]() 时,
时,![]() ,不满足
,不满足![]() ,故
,故![]() ,
,
当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,![]() ,所以
,所以![]()
![]() ,解得
,解得![]() ;
;
当![]() 时,
时,![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() 在
在![]() 上没有最大值,所以
上没有最大值,所以![]() 不满足,
不满足,
综上可得,![]() ;
;
(3)因为![]() ,所以由
,所以由![]() 得
得![]() 令
令![]() ,则
,则![]() ,
,
令![]() 则
则![]() 在
在![]() 上单调递减,且
上单调递减,且![]() ,所以存在唯一的零点
,所以存在唯一的零点![]() ,使得
,使得![]() ,
,
即有![]() 也即有
也即有![]() ,
,![]() ,即
,即![]() ,
,
所以![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上递减,所以
上递减,所以![]() ,
,
而![]() ,所以
,所以![]() ,
,
所以![]() .
.
所以![]() 的取值范围是
的取值范围是![]() .
.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案【题目】据统计,某5家鲜花店今年4月的销售额和利润额资料如下表:
鲜花店名称 | A | B | C | D | E |
销售额x(千元) | 3 | 5 | 6 | 7 | 9 |
利润额y(千元) | 2 | 3 | 3 | 4 | 5 |
(1)用最小二乘法计算利润额y关于销售额x的回归直线方程![]() =
=![]() x+
x+![]() ;
;
(2)如果某家鲜花店的销售额为8千元时,利用(1)的结论估计这家鲜花店的利润额是多少.
参考公式:回归方程![]() 中斜率和截距的最小二乘法估计值公式分别为
中斜率和截距的最小二乘法估计值公式分别为
【题目】一汽车厂生产![]() ,
,![]() ,
,![]() 三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有
三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有![]() 类轿车10辆.
类轿车10辆.
轿车 | 轿车 | 轿车 | |
舒适型 | 100 | 150 |
|
标准型 | 300 | 450 | 600 |
(1)求![]() 的值;
的值;
(2)用分层抽样的方法在![]() 类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从![]() 类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2 把这8辆轿车的得分看作一个总体,从中任取一个得分数
类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2 把这8辆轿车的得分看作一个总体,从中任取一个得分数![]() ,记这8辆轿车的得分的平均数为
,记这8辆轿车的得分的平均数为![]() ,定义事件
,定义事件![]() ,且函数
,且函数![]() 没有零点
没有零点![]() ,求事件
,求事件![]() 发生的概率.
发生的概率.