题目内容
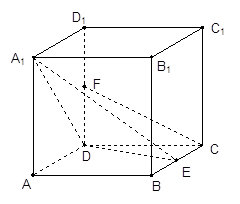
如图,三棱柱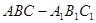 中,
中, ⊥面
⊥面 ,
,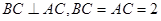 ,
,
 ,
,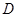 为
为 的中点.
的中点.
(Ⅰ)求证: ;
;
(Ⅱ)求二面角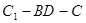 的余弦值;
的余弦值;
(Ⅲ)在侧棱 上是否存在点
上是否存在点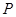 ,使得
,使得
 ?请证明你的结论.
?请证明你的结论.
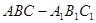 中,
中, ⊥面
⊥面 ,
,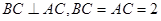 ,
, ,
,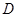 为
为 的中点.
的中点.(Ⅰ)求证:
 ;
;(Ⅱ)求二面角
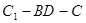 的余弦值;
的余弦值;(Ⅲ)在侧棱
 上是否存在点
上是否存在点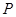 ,使得
,使得 ?请证明你的结论.
?请证明你的结论.
见解析.
第一问中,利用线面平行的判定定理可以得到OD∥B1A,又B1A?平面BDC1,OD⊆平面BDC1
∴B1A∥面BDC1
;第二问中,利用建立空间直角坐标系可以设出法向量,利用法向量的夹角求解二面角的平面角的方法得到。
第三问中,利用假设成立,推出不符合线面垂直的情况,得到一个矛盾,进而得到结论。
(1)证明:连接B1C,交BC1于点O,
则O为B1C的中点,
∵D为AC中点,
∴OD∥B1A,
又B1A?平面BDC1,OD⊆平面BDC1
∴B1A∥面BDC1(4分)
(2)解:∵AA1⊥平面ABC,BC⊥AC,AA1∥CC1,
∴CC1⊥面ABC,
则BC⊥平面AC1,CC1⊥AC
如图建系,则C1(3,0,0),B(0,0,2),D(0,1,0),C(0,0,0)
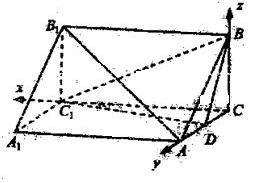
∴ C1D =(-3,1,0), C1B =(-3,0,2)
设平面C1DB的法向量为n=(x,y,z)
则n=(2,6,3)
又平面BDC的法向量为 CC1 =(3,0,0)
∴二面角C1-BD-C的余弦值:cos< CC1,n>= (CC1 .n)/ | CC1 |,|n| ="2/" 7
(3)不存在
(III)假设侧棱AA1上存在一点P(2,y,0)(0≤y≤3),使得CP⊥面BDC1.
则 CP • C1B =0 CP • C1D =0 ,
即 3(y-3)=0
2+3(y-3)=0 ∴方程组无解.∴假设不成立.
∴侧棱AA1上不存在点P,使CP⊥面BDC1.(14分)
∴B1A∥面BDC1
;第二问中,利用建立空间直角坐标系可以设出法向量,利用法向量的夹角求解二面角的平面角的方法得到。
第三问中,利用假设成立,推出不符合线面垂直的情况,得到一个矛盾,进而得到结论。
(1)证明:连接B1C,交BC1于点O,
则O为B1C的中点,
∵D为AC中点,
∴OD∥B1A,
又B1A?平面BDC1,OD⊆平面BDC1
∴B1A∥面BDC1(4分)
(2)解:∵AA1⊥平面ABC,BC⊥AC,AA1∥CC1,
∴CC1⊥面ABC,
则BC⊥平面AC1,CC1⊥AC
如图建系,则C1(3,0,0),B(0,0,2),D(0,1,0),C(0,0,0)

∴ C1D =(-3,1,0), C1B =(-3,0,2)
设平面C1DB的法向量为n=(x,y,z)
则n=(2,6,3)
又平面BDC的法向量为 CC1 =(3,0,0)
∴二面角C1-BD-C的余弦值:cos< CC1,n>= (CC1 .n)/ | CC1 |,|n| ="2/" 7
(3)不存在
(III)假设侧棱AA1上存在一点P(2,y,0)(0≤y≤3),使得CP⊥面BDC1.
则 CP • C1B =0 CP • C1D =0 ,
即 3(y-3)=0
2+3(y-3)=0 ∴方程组无解.∴假设不成立.
∴侧棱AA1上不存在点P,使CP⊥面BDC1.(14分)

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
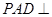 平面
平面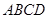 ,
,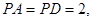 矩形
矩形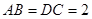 ,
,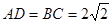 .
.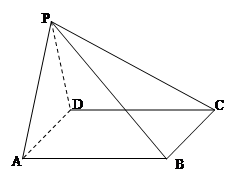
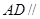 平面
平面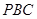 ;
;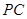 和底面
和底面
 中,
中, 是
是 的中点,
的中点, 是线段
是线段 上一点,且
上一点,且 .
. ;
; 平面
平面 ,求
,求 的值.[
的值.[
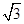 ,AA1=
,AA1=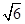 ,M为侧棱CC1上一点,AM⊥BA1。
,M为侧棱CC1上一点,AM⊥BA1。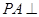 ⊙O,C为圆周上一点,若
⊙O,C为圆周上一点,若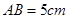 ,
,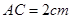 ,则B点到平面PAC的距离为 。
,则B点到平面PAC的距离为 。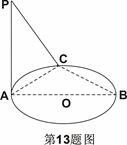




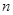
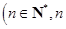 ≥
≥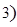 条直线,其中任何两条不平行,任何三条不过同一点,若这
条直线,其中任何两条不平行,任何三条不过同一点,若这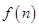 个平面区域,则
个平面区域,则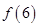 等于( )
等于( )