题目内容
【题目】某电视台举行一个比赛类型的娱乐节目,A、B两队各有六名选手参赛,将他们首轮的比赛成绩作为样本数据,绘制成茎叶图如图所示,为了增加节目的趣味性,主持人故意将A队第六位选手的成绩没有给出,并且告知大家B队的平均分比A队的平均分多4分,同时规定如果某位选手的成绩不少于21分,则获得“晋级”.
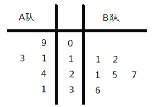
(1)根据茎叶图中的数据,求出A队第六位选手的成绩;
(2)主持人从A队所有选手成绩中随机抽取2个,求至少有一个为“晋级”的概率;
【答案】(1)20;(2)![]() .
.
【解析】
(1)设A队第6位选手的成绩为x,根据题意求出A队、B队的平均值,列平均值式子即可求解.
(2)利用组合数先求出两人都没有“晋级”的概率,再由对立事件的概率计算公式即可求解
(1)B队选手的平均分为![]() ,
,
设A队第6位选手的成绩为x,
则![]() ,
,
得![]() ;
;
(2)A队中成绩不少于21分的有2个,从中抽取2个至少有一个为“晋级”的对立事件为两人都没有“晋级”,其中 A队中![]() 分以下的有
分以下的有![]() 人,
人,![]() 分以上的有
分以上的有![]() 人,所以两人都没有“晋级”,
人,所以两人都没有“晋级”,![]() ,则至少有一个为“晋级”的概率
,则至少有一个为“晋级”的概率![]() .
.

练习册系列答案
相关题目
【题目】某汽车美容公司为吸引顾客,推出优惠活动:对首次消费的顾客,按![]() /次收费,并注册成为会员,对会员逐次消费给予相应优惠,标准如下:
/次收费,并注册成为会员,对会员逐次消费给予相应优惠,标准如下:
消费次第 | 第 | 第 | 第 | 第 |
|
收费比率 |
|
|
|
|
|
该公司注册的会员中没有消费超过![]() 次的,从注册的会员中,随机抽取了100位进行统计,得到统计数据如下:
次的,从注册的会员中,随机抽取了100位进行统计,得到统计数据如下:
消费次数 |
|
|
|
|
|
人数 |
|
|
|
|
|
假设汽车美容一次,公司成本为![]() 元,根据所给数据,解答下列问题:
元,根据所给数据,解答下列问题:
(1)某会员仅消费两次,求这两次消费中,公司获得的平均利润;
(2)以事件发生的频率作为相应事件发生的概率,设该公司为一位会员服务的平均利润为![]() 元,求
元,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.