��Ŀ����
����Ŀ��ijУ�ӲμӸ�һ�꼶���п��Ե�ѧ���������ȡ60��ѧ����������ѧ�ɼ�����Ϊ�������ֳ�����[40��50����[50��60����[90��100]��õ����²���Ƶ�ʷֲ�ֱ��ͼ���۲�ͼ�ε���Ϣ���ش��������⣺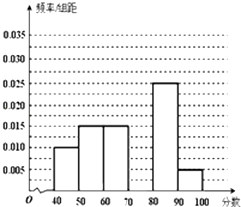
��1���������[70��80���ڵ�Ƶ�ʣ�����ȫ���Ƶ�ʷֲ�ֱ��ͼ��
��2���÷ֲ�����ķ����ڷ�����Ϊ[60��80����ѧ���г�ȡһ������Ϊ6��������������������һ�����壬������ȡ2�ˣ���������1���ڷ�����[70��80���ĸ��ʣ�
���𰸡�
��1��
�⣺������[70��80���ڵ�Ƶ��
1����0.005+0.01+0.015+0.015+0.025+0.005����10=0.3��
�ʳɼ�����[70��80���ϵ�Ƶ����0.3��Ƶ�ʷֲ�ֱ��ͼ����ͼ��
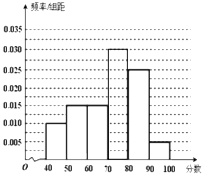
��2��
�⣺�����⣬[60��70�������ε�����Ϊ0.15��60=9�ˣ�[70��80�������ε�����Ϊ0.3��60=18�ˣ�
�߷ֲ�����ڷ�����Ϊ[60��80����ѧ���г�ȡһ������Ϊ6��������
��[60��70�������γ�ȡ2�ˣ��ֱ��Ϊm��n����[70��80�������γ�ȡ4�ˣ��ֱ��Ϊa��b��c��d��
�������ȡ2�ˣ���������1���ڷ�����[70��80��Ϊ�¼�A��
������¼��ռ�����Ļ����¼��У���m��n������m��a������m��b������m��c������m��d��������c��d����15�֣�
������¼�A�����Ļ����¼��У���m��n������m��a������m��b������m��c������m��d������n��a������n��b������n��c������n��d0��9�֣�
��P��A��= ![]()
����������1������Ƶ�ʷֲ�ֱ��ͼ����1��ȥ�ɼ��������������ϵ�Ƶ�ʣ����óɼ�����[70��80���ϵ�Ƶ�ʣ���2���ֱ����[60��70�������ε�������[70��80�������ε������������ùŵ������⣮
�����㾫����������Ҫ�����˷ֲ������Ƶ�ʷֲ�ֱ��ͼ�����֪ʶ�㣬��Ҫ�����Ƚ������е����е�λ����ij���������־���Ա�����ȣ����ֳ��������ͻ��Σ�Ȼ�����ڸ������ͻ����в��ü����������ϵ�ó����İ취��ȡһ���������������Щ���������������������������Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ���Ƕ���ͬ���ݵ����ֲ�ͬ���﷽ʽ.�ý��յı���ı����ݵ����з�ʽ������ʽ����չʾ���ݵķֲ����.ͨ����ͼ�ȿ��Դ���������ȡ��Ϣ���ֿ�������ͼ�δ�����Ϣ������ȷ�����⣮

 ����ͼ���������������ϵ�д�
����ͼ���������������ϵ�д�