题目内容
已知过点A(1,1)且斜率为-m(m>0)的直线l与x、y轴分别交于P、Q两点,过P、Q两点作直线2x+y=0的垂线,垂足为R、S,求四边形PRSQ的面积的最 小值.
四边形PRSQ的面积的最小值为3.6.
设l方程为y-1=-m(x-1),则P(1+ ,0),Q(0,1+m)从而可得直线PR和QS的方程分别为x-2y-
,0),Q(0,1+m)从而可得直线PR和QS的方程分别为x-2y- =0和x-2y+2(m+1)=0.
=0和x-2y+2(m+1)=0.
又PR∥QS,∴|RS|=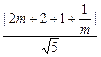 =
= .
.
又|PR|= ,|QS|=
,|QS|= ,四边形PRSQ为梯形,
,四边形PRSQ为梯形,
∴SPRSQ= (
( +
+ )·
)· =
= (m+
(m+ +
+ )2-
)2-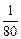 ≥
≥ (2+
(2+ )2-
)2-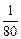 =3.6.
=3.6.
∴四边形PRSQ的面积的最小值为3.6.
 ,0),Q(0,1+m)从而可得直线PR和QS的方程分别为x-2y-
,0),Q(0,1+m)从而可得直线PR和QS的方程分别为x-2y- =0和x-2y+2(m+1)=0.
=0和x-2y+2(m+1)=0.又PR∥QS,∴|RS|=
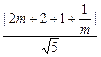 =
= .
.又|PR|=
 ,|QS|=
,|QS|= ,四边形PRSQ为梯形,
,四边形PRSQ为梯形,∴SPRSQ=
 (
( +
+ )·
)· =
= (m+
(m+ +
+ )2-
)2-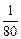 ≥
≥ (2+
(2+ )2-
)2-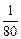 =3.6.
=3.6.∴四边形PRSQ的面积的最小值为3.6.

练习册系列答案
相关题目
 ,-2
,-2
 ,
, ,
,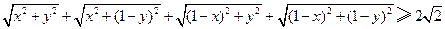 ,并求使等号成立的条件.
,并求使等号成立的条件. ,
, 两点,点
两点,点 内分线段
内分线段 ,且
,且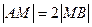 ,求过点
,求过点 的直线的方程.
的直线的方程.