题目内容
(本小题满分14分)
已知在直四棱柱ABCD-A1B1C1D1中,底面ABCD为直角梯形,且满足AD⊥AB,BC∥AD,AD=16,AB=8,BB1=8.E,F分别是线段A1A,BC上的点.
(1)若A1E=5,BF=10,求证:BE∥平面A1FD.
(2)若BD⊥A1F,求三棱锥A1-AB1F的体积.
 |
(1)过E作EG∥AD交A1D于G,连结GF.
∵=,所以=,∴EG=10=BF.
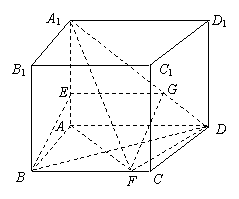 ∵BF∥AD,EG∥AD,∴BF∥EG.
∵BF∥AD,EG∥AD,∴BF∥EG.
∴四边形BFGE是平行四边形.
∴BE∥FG.…………………………………4分
又FGÌ平面A1FD,BEË平面A1FD,
∴BE∥平面A1FD. …………………………………6分
(2)∵在直四棱柱ABCD-A1B1C1D1中,A1A⊥面ABCD,BDÌ面ABCD,∴A1A⊥BD.
由已知,BD⊥A1F,AA1∩A1F=A1,
∴BD⊥面A1AF.
∴BD⊥AF. ………………………………8分
∵梯形ABCD为直角梯形,且满足AD⊥AB,BC∥AD,
∴在Rt△BAD中,tan∠ABD==2.
在Rt△ABF中,tan∠BAF==.
∵BD⊥AF,∴∠ABD+∠BAF=,∴=,BF=4. ………………10分
∵在直四棱柱ABCD-A1B1C1D1中,A1A⊥面ABCD,
∴面AA1B1B⊥面ABCD,又面ABCD∩面AA1B1B=AB,∠ABF=90°,
∴FB⊥面AA1B1B,即BF为三棱锥F-A1B1A的高. ………………12分
∵∠AA1B1=90°,AA1=BB1=8,A1B1=AB=8,∴S=32.
∴V=V=×S×BF=. ………………14分

 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)