Question

【题目】点P在圆O：x2+y2=8上运动，PD⊥x轴，D为垂足，点M在线段PD上，满足 ．
（1）求点M的轨迹方程；
（2）过点Q（1， ）作直线l与点M的轨迹相交于A、B两点，使点Q为弦AB的中点，求直线l的方程．

Answer 1

【答案】
（1）解：∵点M在线段PD上，满足 ，

∴点M是线段PD的中点，

设M（x，y），则P（x，2y），

∵点P在圆O：x2+y2=8上运动，

则x2+（2y）2=8，

即 ，

故点M的轨迹方程为 ．

（2）解：

方法一：当直线l⊥x轴时，由椭圆的对称性可得弦AB的中点在x轴上，

不可能是点Q，这种情况不满足题意．

设直线l的方程为 ，

由 ，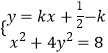

可得 ，

由韦达定理可得x1+x2=﹣ ，

由AB的中点为 ，可得﹣ =2，

解得 ，

即直线l的方程为y﹣ =﹣ （x﹣1），

则直线l的方程为x+2y﹣2=0．

方法二：当直线l⊥x轴时，由椭圆的对称性可得弦AB的中点在x轴上，

不可能是点Q，这种情况不满足题意．

设A（x1，y1），B（x2，y2），

A、B两点在椭圆上，

满足 ，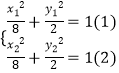

由（1）﹣（2）可得 ，

则 ，

由AB的中点为 ，可得x1+x2=2，y1+y2=1，代入上式 ，

即直线l的方程为y﹣ =﹣ （x﹣1），

∴直线l的方程为x+2y﹣2=0．

【解析】（1）判断M线段PD的中点，设M（x，y），则P（x，2y），运用代入法，即可得到所求轨迹方程；（2） 方法一、运用直线方程和椭圆方程联立，运用韦达定理和中点坐标公式，化简整理可得斜率k，由点斜式方程可得直线方程；
方法二、设A（x1 ， y1），B（x2 ， y2），A、B两点在椭圆上，代入椭圆方程，运用作差法和斜率公式，再由点斜式方程可得直线的方程．