题目内容
【题目】已知函数f（x）= 
+lnx在（1，+∞）上是增函数，且a＞0．
（1）求a的取值范围；
（2）求函数g（x）=ln（1+x）﹣x在[0，+∞）上的最大值；
（3）设a＞1，b＞0，求证： 
．
【答案】
（1）解：f（x）的导数为f′（x）=﹣ 
+ 
，
因为函数f（x）在（1，+∞）上是增函数，
所以f′（x）=﹣ + ≥0在（1，+∞）上恒成立，
即x≥ 
在（1，+∞）上恒成立，
所以只需1≥ ，
又因为a＞0，所以a≥1
（2）解：因为x∈[0，+∞），所以g′（x）= 
﹣1= 
≤0
所以g（x）在[0，+∞）上单调递减，
所以g（x）=ln（1+x）﹣x在[0，+∞）上的最大值为g（0）=0
（3）解：证明：因为a＞1，b＞0，所以 
＞1，
由（1）知f（x）= 
+lnx在（1，+∞）上是增函数，所以f（ ）＞f（1），
即 
+ln ＞0，化简得 
＜ln ，
又因为 =1+ 
，
由第（2）问可知g（ ）=ln（1+ ）﹣ ＜g（0）=0，
即ln ＜ ，
综上 
得证
【解析】（1）求出函数的导数，由函数f（x）在（1，+∞）上是增函数，所以f′（x）=﹣ + ≥0在（1，+∞）上恒成立，运用参数分离，求得最值即可；（2）求得g（x）的导数，求得单调性，即可得到最小值；（3）由（1）知f（x）= +lnx在（1，+∞）上是增函数，所以f（ ）＞f（1），由第（2）问可知g（ ）=ln（1+ ）﹣ ＜g（0）=0，化简即可得证．
【考点精析】通过灵活运用利用导数研究函数的单调性和函数的最大(小)值与导数，掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间
内，(1)如果
，那么函数
在这个区间单调递增；(2)如果
，那么函数
在这个区间单调递减；求函数在
上的最大值与最小值的步骤：（1）求函数在内的极值；（2）将函数的各极值与端点处的函数值
，
比较，其中最大的是一个最大值，最小的是最小值即可以解答此题．
【题目】某地区2007年至2013年农村居民家庭人均纯收入y（单位：千元）的数据如表：
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
（Ⅰ）求y关于t的线性回归方程；
（Ⅱ）利用（Ⅰ）中的回归方程，分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入．
附：回归直线的斜率和截距的最小二乘估计公式分别为： 
= 
， 
= 
﹣ 
．
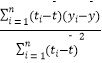