题目内容
12. 如图,在长方体ABCD-A1B1C1D1中,AA1=1,AB=AD=2,E、F分别是AB、BC的中点,证明A1、C1、F、E四点共面,并求直线CD1与平面A1C1FE所成的角的大小.
如图,在长方体ABCD-A1B1C1D1中,AA1=1,AB=AD=2,E、F分别是AB、BC的中点,证明A1、C1、F、E四点共面,并求直线CD1与平面A1C1FE所成的角的大小.
分析 利用长方体的几何关系建立直角坐标系.利用向量方法求空间角.
解答 解:连接AC,因为E,F分别是AB,BC的中点,所以EF是△ABC的中位线,所以EF∥AC.由长方体的性质知AC∥A1C1,
所以EF∥A1C1,
所以A1、C1、F、E四点共面.
以D为坐标原点,DA、DC、DD1分别为x、y、z轴,建立空间直角坐标系,易求得
$\overrightarrow{{D}_{1}C}=(0,2,-1)$
$\overrightarrow{{A}_{1}{C}_{1}}=(-2,2,0)$,$\overrightarrow{{A}_{1}E}=(0,1,-1)$
设平面A1C1EF的法向量为$\overrightarrow{n}=(x,y,z)$
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{{A}_{1}{C}_{1}}=0}\\{\overrightarrow{n}•\overrightarrow{{A}_{1}E}=0}\end{array}\right.$,所以$\left\{\begin{array}{l}{(x,y,z)•(-2,2,0)=0}\\{(x,y,z)(0,1,-1)=0}\end{array}\right.$,即$\left\{\begin{array}{l}{-2x+2y=0}\\{y-z=0}\end{array}\right.$,
z=1,得x=1,y=1,所以$\overrightarrow{n}=(1,1,1)$,
所以$|cos<\overrightarrow{n},\overrightarrow{{D}_{1}C}>|=\frac{|\overrightarrow{n}•\overrightarrow{{D}_{1}C}|}{|\overrightarrow{n}||\overrightarrow{{D}_{1}C}|}$=$\frac{|(1,1,1)•(0,2,-1)|}{\sqrt{3}\sqrt{5}}=\frac{\sqrt{15}}{15}$,
所以直线CD1与平面A1C1FE所成的角的大小arcsin$\frac{\sqrt{15}}{15}$.
点评 本题主要考查利用空间直角坐标系求出空间角的方法,属高考常考题型.

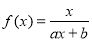 (
(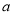 ,
,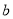 为常数,
为常数, )满足
)满足 ,且
,且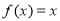 有唯一解.
有唯一解.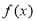 的解析式;
的解析式; ,且
,且 (
( ,
, ),求证:数列
),求证:数列 为等差数列.
为等差数列.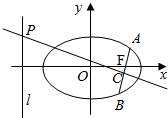 如图,在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且右焦点F到左准线l的距离为3.
如图,在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且右焦点F到左准线l的距离为3.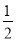 ,
,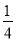 ,
,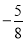 ,
,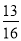 ,
,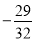 ,
,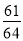 ,…
,…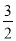 ,1,
,1,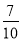 ,
,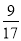 ,…
,…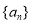 满足:
满足: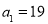 ,
,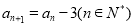 ,而数列
,而数列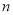 项和数值最大时,
项和数值最大时,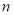 的值为( )
的值为( ) 中,内角
中,内角 ,
,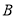 ,
,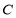 的对边分别为
的对边分别为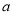 ,
,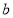 ,
,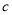 ,且
,且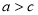 ,已知
,已知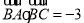 ,
,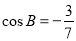 ,
,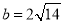 .求:
.求: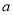 和
和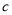 的值;
的值;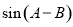 的值.
的值.