题目内容
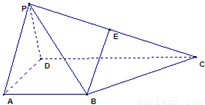
如图，在四棱锥P-ABCD中，E为PC的中点．，侧面PAD是等边三角形，底面ABCD是梯形，且AB∥CD，CD=2AB．（1）证明：直线BE∥平面PAD；
（2）求异面直线AD和BE所成的角．
【答案】分析：（1）取PD中点F，连结EF、AF，利用三角形中位线定理及梯形梯形ABCD中，AB∥CD且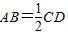
，证出四边形ABEF为平行四边形，BE∥AF，结合线面平行的判定定理即可得到BE∥平面PAD；
（2）根据异面直线所成角的定义，得∠FAD就是异面直线AD与BE的所成角．由AF是正△PAD的中线得到∠FAD=30°，从而得到异面直线AD与BE的所成角为30°．
解答：解：（1）取PD中点F，连结EF、AF，
∵EF是△PCD的中位线，可得EF∥CD，且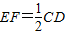
…（2分）
又∵梯形ABCD中，AB∥CD，且
∴EF∥AB且EF=AB，可得四边形ABEF为平行四边形，
∴BE∥AF，…（4分）
∵BE?平面PAD，AF?平面PAD，∴BE∥平面PAD；…（6分）
（2）由（1）可知BE∥AF，
∴∠FAD就是异面直线AD与BE的所成角，…（ 10分）
∵△PAD是正三角形，且AF是中线，∴∠FAD=30°，
即异面直线AD与BE的所成角为30°…（12分）
点评：本题在四棱锥中求证线面平行，并求异面直线所成的角大小，着重考查了线面平行的判定定理与异面直线所成角的定义及求法等知识，属于中档题．
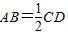，证出四边形ABEF为平行四边形，BE∥AF，结合线面平行的判定定理即可得到BE∥平面PAD；（2）根据异面直线所成角的定义，得∠FAD就是异面直线AD与BE的所成角．由AF是正△PAD的中线得到∠FAD=30°，从而得到异面直线AD与BE的所成角为30°．
解答：解：（1）取PD中点F，连结EF、AF，
∵EF是△PCD的中位线，可得EF∥CD，且
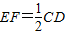…（2分）又∵梯形ABCD中，AB∥CD，且
∴EF∥AB且EF=AB，可得四边形ABEF为平行四边形，
∴BE∥AF，…（4分）
∵BE?平面PAD，AF?平面PAD，∴BE∥平面PAD；…（6分）
（2）由（1）可知BE∥AF，
∴∠FAD就是异面直线AD与BE的所成角，…（ 10分）
∵△PAD是正三角形，且AF是中线，∴∠FAD=30°，
即异面直线AD与BE的所成角为30°…（12分）
点评：本题在四棱锥中求证线面平行，并求异面直线所成的角大小，着重考查了线面平行的判定定理与异面直线所成角的定义及求法等知识，属于中档题．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
如图，在四棱锥P-ABCD中，底面ABCD是矩形．已知AB=3，AD=2，PA=2，PD=2
如图，在四棱锥P-ABCD中，PA⊥平面ABCD，四边形ABCD为正方形，AB=4，PA=3，点A在PD上的射影为点G，点E在AB上，平面PEC⊥平面PDC．
如图，在四棱锥P-ABCD中，PA⊥底面ABCD，∠BCD=120°，BC⊥AB，CD⊥AD，BC=CD=PA=a，
如图，在四棱锥P-ABCD中，底面是边长为a的菱形，∠ABC=60°PD⊥面ABCD，PC=a，E为PB中点
（2008•武汉模拟）如图，在四棱锥P-ABCD中，底面ABCD是直角梯形，BC∥AD，且∠BAD=90°，又PA⊥底面ABCD，BC=AB=PA=1，AD=2．