题目内容
11.设F为抛物线C:y2=3x的焦点,过F且倾斜角为30°的直线交抛物线C于A,B两点,则|AB|=12.分析 由抛物线方程求出焦点坐标,由直线的倾斜角求出斜率,写出过A,B两点的直线方程,和抛物线方程联立后化为关于x的一元二次方程,由根与系数关系得到A,B两点横坐标的和,代入抛物线过焦点的弦长公式得答案.
解答 解:由y2=3x,得2p=3,p=$\frac{3}{2}$,
则F($\frac{3}{4}$,0),
∴过A,B的直线方程为y=$\frac{\sqrt{3}}{3}$(x-$\frac{3}{4}$),
联立$\left\{\begin{array}{l}{{y}^{2}=3x}\\{y=\frac{\sqrt{3}}{3}(x-\frac{3}{4})}\end{array}\right.$,得16x2-168x+9=0.
设A(x1,y1),B(x2,y2),
则${x}_{1}+{x}_{2}=\frac{168}{16}=\frac{21}{2}$,
∴|AB|=${x}_{1}+{x}_{2}+p=\frac{21}{2}+\frac{3}{2}=12$.
故答案为:12.
点评 本题考查直线与圆锥曲线的关系,考查数学转化思想方法,涉及直线和圆锥曲线关系问题,常采用联立直线和圆锥曲线,然后利用一元二次方程的根与系数关系解题,是中档题.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
19.已知抛物线C:x2=16y的焦点为F,准线为l,M是l上一点,P是直线MF与C的一个交点,若$\overrightarrow{FM}$=3$\overrightarrow{FP}$,则|PF|=( )
| A. | $\frac{16}{3}$ | B. | $\frac{8}{3}$ | C. | $\frac{5}{3}$ | D. | $\frac{5}{2}$ |
16.已知函数f(x)=lg$\frac{1+x}{1-x}$,则“x<$\frac{9}{11}$”是“f(x)<1成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
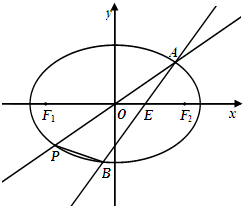 如图,在平面直角坐标系xoy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,直线l与x轴交于点E,与椭圆C交于A、B两点.当直线l垂直于x轴且点E为椭圆C的右焦点时,弦AB的长为$\frac{{2\sqrt{6}}}{3}$.
如图,在平面直角坐标系xoy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,直线l与x轴交于点E,与椭圆C交于A、B两点.当直线l垂直于x轴且点E为椭圆C的右焦点时,弦AB的长为$\frac{{2\sqrt{6}}}{3}$.