题目内容
从编号为1,2,3,4,5,6,7,8,9,10的十个形状大小相同的球中,任取3个球,则这3个球编号之和为奇数的概率是 .
【答案】分析:根据题意,由组合数公式计算可得从10个球中任取3个球的取法数目,再分2种情况讨论取出的3个球编号之和为奇数的情况,由分类加法计数原理计算可得取出的3个球编号之和为奇数的取法数目,由等可能事件的概率公式,计算可得答案.
解答:解:根据题意,从10个球中任取3个球,有C103=120种取法,若取出的3个球编号之和为奇数,有2种情况,
①,取出的3个球编号均为奇数,有C53=10种取法,
②,取出的3个球编号为1个奇数,2个偶数,有C51×C52=50种取法,
则取出的3个球编号之和为奇数的取法有10+50=60种,
则其概率为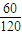 =
= ,
,
故答案为 .
.
点评:本题考查等可能事件计算,解题时要分情况讨论3个球编号之和为奇数,要结合代数知识来解题.
解答:解:根据题意,从10个球中任取3个球,有C103=120种取法,若取出的3个球编号之和为奇数,有2种情况,
①,取出的3个球编号均为奇数,有C53=10种取法,
②,取出的3个球编号为1个奇数,2个偶数,有C51×C52=50种取法,
则取出的3个球编号之和为奇数的取法有10+50=60种,
则其概率为
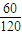 =
= ,
,故答案为
 .
.点评:本题考查等可能事件计算,解题时要分情况讨论3个球编号之和为奇数,要结合代数知识来解题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目