题目内容
【题目】已知定义在![]() 上的函数
上的函数![]() 的图像是一条连续不断的曲线,且在任意区间上
的图像是一条连续不断的曲线,且在任意区间上![]() 都不是常值函数.设
都不是常值函数.设![]() ,其中分点
,其中分点![]() 将区间
将区间![]() 任意划分成
任意划分成![]() 个小区间
个小区间![]() ,记
,记![]() ,称为
,称为![]() 关于区间
关于区间![]() 的
的![]() 阶划分“落差总和”.
阶划分“落差总和”.
当![]() 取得最大值且
取得最大值且![]() 取得最小值
取得最小值![]() 时,称
时,称![]() 存在“最佳划分”
存在“最佳划分”![]() .
.
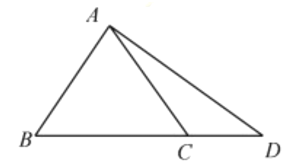
(1)已知![]() ,求
,求![]() 的最大值
的最大值![]() ;
;
(2)已知![]() ,求证:
,求证:![]() 在
在![]() 上存在“最佳划分”
上存在“最佳划分”![]() 的充要条件是
的充要条件是![]() 在
在![]() 上单调递增.
上单调递增.
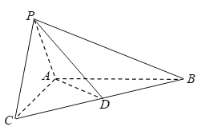
(3)若![]() 是偶函数且存在“最佳划分”
是偶函数且存在“最佳划分”![]() ,求证:
,求证:![]() 是偶数,且
是偶数,且![]() .
.
【答案】(1)3;(2)见解析;(3)见解析
【解析】
(1)直接利用题中给的定义求解即可;
(2)利用函数的单调性和数列的信息应用求出充要条件;
(3)利用函数的奇偶性和存在的最佳划分,进一步建立函数的单调区间,最后求出函数的关系式.
(1)![]() ;
;
(2)若![]() 在
在![]() 上单调递增,则
上单调递增,则![]() ,
,
故![]() 在
在![]() 上存在“最佳划分”
上存在“最佳划分”![]()
若![]() 在
在![]() 上存在“最佳划分”
上存在“最佳划分”![]() ,倘若
,倘若![]() 在
在![]() 上不单调递增,
上不单调递增,
则存在![]() .
.
由![]() (*)
(*)
等号当且仅当![]() 时取得,此时
时取得,此时
![]() ,与题设矛盾,舍去,故(*)式中等号不成立,即:增加分点
,与题设矛盾,舍去,故(*)式中等号不成立,即:增加分点![]() 后,“落差总和”会增加,故
后,“落差总和”会增加,故![]() 取最大值时
取最大值时![]() 的最小值大于1,与条件矛盾.
的最小值大于1,与条件矛盾.
所以![]() 在
在![]() 上单调递增;
上单调递增;
(3)由(2)的证明过程可知,在任间区间![]() 上,若
上,若![]() 存在最佳划分
存在最佳划分![]() ,则当
,则当![]() 时,
时,![]() 为常值函数(舍);当
为常值函数(舍);当![]() 时,
时,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() 单调递减,
单调递减,
若![]() 在
在![]() 上存在最佳划分
上存在最佳划分![]() ,则此时在每个小区间
,则此时在每个小区间![]() 上均为最佳划分
上均为最佳划分![]() .否则,添加分点后可使
.否则,添加分点后可使![]() 在
在![]() 上的“落差总和”增大,从而
上的“落差总和”增大,从而![]() 不是“落差总和”的最大值,与“
不是“落差总和”的最大值,与“![]() 在
在![]() 上存在最佳划分
上存在最佳划分![]() ”矛盾,故
”矛盾,故![]() 在每个小区间
在每个小区间![]() 上都是单调,
上都是单调,
若![]() 在
在![]() 上存在最佳划分
上存在最佳划分![]() ,则
,则![]() 在相邻的两个区间
在相邻的两个区间![]() 上具有不同的单调性,否则,
上具有不同的单调性,否则,![]() ,
,
减少分点![]() ,“落差总和”的值不变,而
,“落差总和”的值不变,而![]() 的值减少1,故
的值减少1,故![]() 的最小值不是
的最小值不是![]() ,与“
,与“![]() 在
在![]() 上存在最佳划分
上存在最佳划分![]() ”矛盾,
”矛盾,
![]() 存在“最佳划分”
存在“最佳划分”![]() ,故
,故![]() 在每个小区间
在每个小区间![]() 上都单调,而
上都单调,而![]() 是偶函数,故
是偶函数,故![]() 在
在![]() 轴两侧的单调区间对称,共有偶数个单调区间,且当
轴两侧的单调区间对称,共有偶数个单调区间,且当![]() 时,
时,![]() ,从而有
,从而有![]() .
.

【题目】近年来,共享单车已经悄然进入了广大市民的日常生活,并慢慢改变了人们的出行方式.为了更好地服务民众,某共享单车公司在其官方![]() 中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价,现从评价系统中选出
中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价,现从评价系统中选出![]() 条较为详细的评价信息进行统计,车辆状况和优惠活动评价的
条较为详细的评价信息进行统计,车辆状况和优惠活动评价的![]() 列联表如下:
列联表如下:
对优惠活动好评 | 对优惠活动不满意 | 合计 | |
对车辆状况好评 |
|
|
|
对车辆状况不满意 |
|
|
|
合计 |
|
|
|
(1)能否在犯错误的概率不超过![]() 的前提下认为优惠活动好评与车辆状况好评之间有关系?
的前提下认为优惠活动好评与车辆状况好评之间有关系?
(2)为了回馈用户,公司通过![]() 向用户随机派送骑行券,用户可以将骑行券用于骑行付费,也可以通过
向用户随机派送骑行券,用户可以将骑行券用于骑行付费,也可以通过![]() 转赠给好友某用户共获得了
转赠给好友某用户共获得了![]() 张骑行券,其中只有
张骑行券,其中只有![]() 张是一元券现该用户从这张骑行券中随机选取
张是一元券现该用户从这张骑行券中随机选取![]() 张转赠给好友,求选取的
张转赠给好友,求选取的![]() 张中至少有
张中至少有![]() 张是一元券的概率.
张是一元券的概率.
附:下面的临界值表仅供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考公式: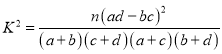 ,其中
,其中![]() )
)