题目内容
(5分)(2011•天津)已知双曲线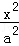 ﹣
﹣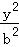 =1(a>0,b>0)的左顶点与抛物线y2=2px的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(﹣2,﹣1),则双曲线的焦距为( )
=1(a>0,b>0)的左顶点与抛物线y2=2px的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(﹣2,﹣1),则双曲线的焦距为( )
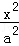 ﹣
﹣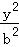 =1(a>0,b>0)的左顶点与抛物线y2=2px的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(﹣2,﹣1),则双曲线的焦距为( )
=1(a>0,b>0)的左顶点与抛物线y2=2px的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(﹣2,﹣1),则双曲线的焦距为( )A.2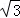 | B.2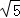 | C.4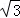 | D.4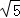 |
B
试题分析:根据题意,点(﹣2,﹣1)在抛物线的准线上,结合抛物线的性质,可得p=4,进而可得抛物线的焦点坐标,依据题意,可得双曲线的左顶点的坐标,即可得a的值,由点(﹣2,﹣1)在双曲线的渐近线上,可得渐近线方程,进而可得b的值,由双曲线的性质,可得c的值,进而可得答案.
解:根据题意,双曲线的一条渐近线与抛物线的准线的交点坐标为(﹣2,﹣1),
即点(﹣2,﹣1)在抛物线的准线上,又由抛物线y2=2px的准线方程为x=﹣
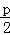 ,则p=4,
,则p=4,则抛物线的焦点为(2,0);
则双曲线的左顶点为(﹣2,0),即a=2;
点(﹣2,﹣1)在双曲线的渐近线上,则其渐近线方程为y=±
 x,
x,由双曲线的性质,可得b=1;
则c=
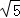 ,则焦距为2c=2
,则焦距为2c=2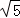 ;
;故选B.
点评:本题考查双曲线与抛物线的性质,注意题目“双曲线的一条渐近线与抛物线的准线的交点坐标为(﹣2,﹣1)”这一条件的运用,另外注意题目中要求的焦距即2c,容易只计算到c,就得到结论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的右支上一点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,下列命题正确的是( ).
的右支上一点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,下列命题正确的是( ). ;
; ,则e的最大值为
,则e的最大值为 ;
; .
.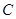 经过点(2,2),且与
经过点(2,2),且与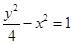 具有相同渐近线,则
具有相同渐近线,则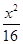 -
-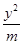 =1的离心率为
=1的离心率为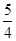 ,则m等于________.
,则m等于________.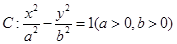 的两个焦点为
的两个焦点为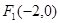 、
、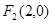 点
点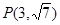 在双曲线C上.
在双曲线C上.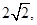 求直线l的方程.
求直线l的方程.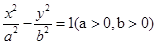 的左、右焦点分别是
的左、右焦点分别是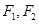 ,过
,过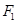 作倾斜角为
作倾斜角为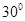 的直线交双曲线右支于点M,若
的直线交双曲线右支于点M,若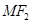 垂直于x轴,则双曲线的离心率为( )
垂直于x轴,则双曲线的离心率为( )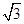
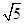
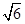
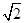
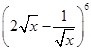 的展开式中含
的展开式中含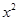 项的系数是
项的系数是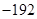 ;
;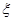 服从正态分布N(2,
服从正态分布N(2,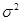 )(
)(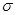 >0).若
>0).若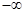 ,1)内取值的概率为0.15,则
,1)内取值的概率为0.15,则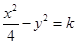 的渐近线方程为
的渐近线方程为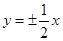 ,则k=1.其中正确命题的序号是 .
,则k=1.其中正确命题的序号是 .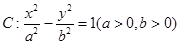 的左、右焦点分别是
的左、右焦点分别是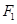 、
、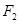 过
过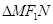 为正三角形,则该双曲线的离心率为( )
为正三角形,则该双曲线的离心率为( )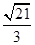
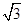
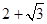
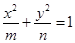
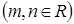 的右焦点与抛物线
的右焦点与抛物线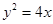 的焦点重合,
的焦点重合,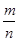 ="____________" .
="____________" .