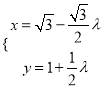题目内容
【题目】平面直角坐标系中,有椭圆 (
(![]() 为参数)和抛物线
为参数)和抛物线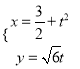 (
(![]() 为参数).
为参数).
(Ⅰ)是否存在这样的![]() 值,使得该椭圆与该抛物线有四个不同的交点?请说明理由.
值,使得该椭圆与该抛物线有四个不同的交点?请说明理由.
(Ⅱ)当![]() 取何值时,该椭圆与该抛物线的交点与坐标原点的距离等于这个交点与该椭圆中心的距离?
取何值时,该椭圆与该抛物线的交点与坐标原点的距离等于这个交点与该椭圆中心的距离?
【答案】(1)不存在(2)0或 ![]() .
.
【解析】试题分析:(1)将题中的椭圆及抛物线方程分别消参化为普通方程,并联立得方程组,转化为二次方程根的分布问题;(2)确定该椭圆与该抛物线的交点与坐标原点的距离,确定这个交点与该椭圆中心的距离,比较判断即可.
试题解析:
解:(Ⅰ)将题中的椭圆及抛物线方程分别消参化为普通方程,并联立得方程组: 
消去y得![]() ,令
,令![]() .
.
由抛物线方程知![]() ,则椭圆与抛物线有四个交点的充要条件是方程
,则椭圆与抛物线有四个交点的充要条件是方程![]()
在![]() 上有两个不等的实根,即
上有两个不等的实根,即 即
即
显然此不等式组无解,故满足题设条件的![]() 值不存在.
值不存在.
(Ⅱ)由Δ≥0得![]() ,又知椭圆的半长轴
,又知椭圆的半长轴![]() ,抛物线的顶点为
,抛物线的顶点为![]() ,故当
,故当![]() ,即
,即![]() 时,椭圆与抛物线必相交.
时,椭圆与抛物线必相交.
若满足题设条件,可有以下两种情况:①椭圆中心与原点重合,此时![]() ;②椭圆与抛物线的交点在椭圆中心与原点所连线段的垂直平分线上,即交点在直线
;②椭圆与抛物线的交点在椭圆中心与原点所连线段的垂直平分线上,即交点在直线![]() 上,
上,
将![]() 代入
代入![]() ,得
,得![]() ,解得
,解得![]() 舍去负值).
舍去负值).
综上所述,满足题设条件的![]() 值应为0或
值应为0或 ![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目