题目内容
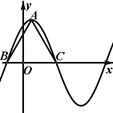
函数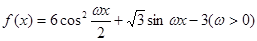 在一个周期内的图象如图所示,
在一个周期内的图象如图所示, 为
为
图象的最高点, 、
、 为图象与
为图象与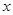 轴的交点,且
轴的交点,且 为正三角形.
为正三角形.
(Ⅰ)求 的值及函数
的值及函数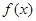 的值域;
的值域;
(Ⅱ)若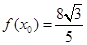 ,且
,且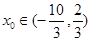 ,求
,求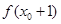 的值.
的值.
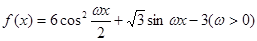 在一个周期内的图象如图所示,
在一个周期内的图象如图所示,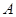 为
为图象的最高点,
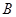 、
、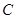 为图象与
为图象与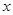 轴的交点,且
轴的交点,且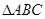 为正三角形.
为正三角形.
(Ⅰ)求
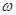 的值及函数
的值及函数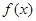 的值域;
的值域;(Ⅱ)若
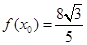 ,且
,且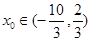 ,求
,求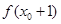 的值.
的值.(Ⅰ函数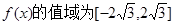 ;(Ⅱ)
;(Ⅱ)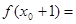
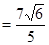 .
.
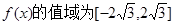 ;(Ⅱ)
;(Ⅱ)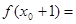
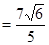 .
. 试题分析:(Ⅰ)由已知可得:
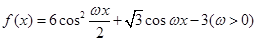
=3cosωx+
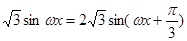
又由于正三角形ABC的高为2
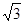 ,则BC="4"
,则BC="4" 所以,函数
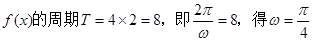
所以,函数
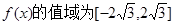 7分
7分(Ⅱ)因为
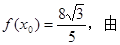 (Ⅰ)有
(Ⅰ)有 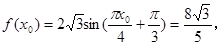

由x0
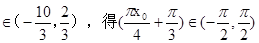
所以,
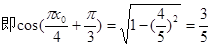
故
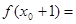
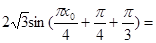
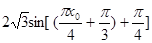
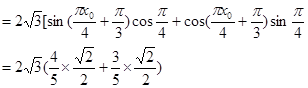
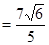 . 14分
. 14分点评:典型题,本题首先根据给定图象,确定得到三角函数式,为研究三角函数的图象和性质,由利用三角函数和差倍半公式等,将函数“化一”,这是常考题型。首先运用“三角公式”进行化简,为进一步解题奠定了基础。(2)利用整体代换思想,通过变角应用两角和差的三角函数公式,计算得到函数值。

练习册系列答案
相关题目
 π
π π
π
 .
. 的定义域及最小正周期;
的定义域及最小正周期;
 上的最值.
上的最值. 的最小正周期为( )
的最小正周期为( )


 的图像上的每一点的横坐标伸长为原来的2倍,纵坐标不变,然后再向左平移
的图像上的每一点的横坐标伸长为原来的2倍,纵坐标不变,然后再向左平移 个单位后得到一个最小正周期为
个单位后得到一个最小正周期为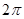 的奇函数
的奇函数 。
。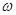 和
和 的值
的值 的最大值与最小值。
的最大值与最小值。 是 ( )
是 ( ) 的偶函数
的偶函数 的偶函数
的偶函数 ,且α是第二象限角,那么sin 2α=________.
,且α是第二象限角,那么sin 2α=________.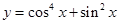 的周期是 ( )
的周期是 ( )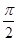
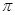
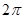
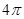
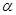 ,tan
,tan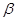 是方程
是方程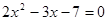 的两根,则tan(
的两根,则tan(