题目内容
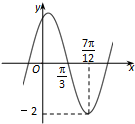函数f（x）=Asin（ωx+φ）（A＞0，ω＞0）的部分图象如图所示，下列结论：①将f（x）的图象向左平移
| π |
| 6 |
②f（x）的最小正周期为π；
③f（0）=1；
④f（
| 12π |
| 11 |
| 14π |
| 13 |
⑤f（x）=-f（
| 5π |
| 3 |
其中正确的是（ ）
分析：函数f（x）=Asin（ωx+φ）图象可求得其解析式，从而可判断②③⑤的正误，再由正弦函数的单调性可判断④，由三角函数的图象变换规律可判断①，从而可得答案．
解答：解：由图知，A=2，
=
-
=
，
∴T=π=
，
∴ω=2；
又
×2+φ=π，
∴φ=
；
∴f（x）=2sin（2x+
）．
∴f（x+
）=2sin[2（x+
）+
]=2sin（2x+
），显然不是偶函数，故①错误；
∴f（x）的最小正周期为π，②正确；
f（0）=2sin
=
≠1，③错误；
f（
）=2sin（2×
+
）=2sin
=2sin
，
同理可求f（
）=2sin
；
∵
-
=
=
＜0，
即0＜
＜
＜
，由y=sinx在[0，
]上单调递增可知，f（
）＜f（
），即④正确；
又f（
-x）=2sin[2（
-x）+
]=2sin（
-2x）=2sin[4π-（2x+
）]=2sin[-（2x+
）]=-sin（2x+
）=-f（x），
∴f（x）=-f（
-x），即⑤正确；
∴正确的是②④⑤．
故选D．
，A=2，| T |
| 4 |
| 7π |
| 12 |
| π |
| 3 |
| π |
| 4 |
∴T=π=
| 2π |
| ω |
∴ω=2；
又
| π |
| 3 |
∴φ=
| π |
| 3 |
∴f（x）=2sin（2x+
| π |
| 3 |
∴f（x+
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
∴f（x）的最小正周期为π，②正确；
f（0）=2sin
| π |
| 3 |
| 3 |
f（
| 12π |
| 11 |
| 12π |
| 11 |
| π |
| 3 |
| 17π |
| 33 |
| 16π |
| 33 |
同理可求f（
| 14π |
| 13 |
| 19π |
| 39 |
∵
| 16π |
| 33 |
| 19π |
| 39 |
| 16π×39-19π×33 |
| 33×39 |
| 624π-627π |
| 33×39 |
即0＜
| 16π |
| 33 |
| 19π |
| 39 |
| π |
| 2 |
| π |
| 2 |
| 12π |
| 11 |
| 14π |
| 13 |
又f（
| 5π |
| 3 |
| 5π |
| 3 |
| π |
| 3 |
| 11π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
∴f（x）=-f（
| 5π |
| 3 |
∴正确的是②④⑤．
故选D．
点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，考查正弦函数的单调性与周期性，考查三角函数的图象变换，求得y=Asin（ωx+φ）的其解析式是关键，属于中档题．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0）的部分图象如图所示，则f（1）+f（2）+f（3）+…+f（2008）的值等于
函数f（x）=Asin（ωx+?）（其中A＞0，ω＞0，
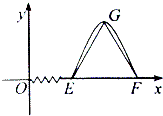已知函数f（x）=Asinωx（A＞0，ω＞0）的部分图象如图所示，若△EFG是边长为2的正三角形，则f（1）=（ ）A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|