题目内容
【题目】已知圆
的圆心在直线
上．
（Ⅰ）若圆C与y轴相切，求圆C的方程；
（Ⅱ）当a=0时，问在y轴上是否存在两点A，B，使得对于圆C上的任意一点P，都有
，若有，试求出点A，B的坐标，若不存在，请说明理由．
【答案】（Ⅰ）
，或
;（Ⅱ）存在两点A（0，﹣2）、B（0，0），或A（0，4）、B（0，2）.
【解析】
（Ⅰ）由圆与y轴相切，求出|a|＝
；（Ⅱ）假设存在满足题意的A、B、P，设出这三个点的坐标，然后由两点间的距离公式将几何条件|PA|＝|PB坐标化，整理后对y恒成立两边对应项系数相等，列方程组解出y1，y2，即可求出．
（I）∵圆
的圆心
在直线
上，
∴
，∵圆C与y轴相切，∴
，
∴
，
，
故所求圆C的方程，或，
（II）∵a=0，
，
∴圆的方程为
，∴
，
假设在y轴上存在两点
，使得对于圆C上的任意一点P，都有
，设
，则由得 
，
∴
，
，
依题意此方程对y恒成立，故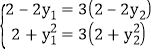
，
解得
或
，
故在y轴上存在两点A（0，﹣2）、B（0，0），或A（0，4）、B（0，2），使得对于圆C上的任意一点P，都有．
【题目】据统计，仅在北京地区每天就有500万单快递等待派送，近5万多名快递员奔跑在一线，快递网点人员流动性也较强，各快递公司需要经常招聘快递员，保证业务的正常开展.下面是50天内甲、乙两家快递公司的快递员的每天送货单数统计表：
送货单数 | 30 | 40 | 50 | 60 | |
天数 | 甲 | 10 | 10 | 20 | 10 |
乙 | 5 | 15 | 25 | 5 | |
已知这两家快递公司的快递员的日工资方案分别为：甲公司规定底薪
元，每单抽成
元；乙公司规定底薪
元，每日前
单无抽成，超过单的部分每单抽成
元．
（1）分别求甲、乙快递公司的快递员的日工资
（单位：元）与送货单数
的函数关系式；
（2）若将频率视为概率，回答下列问题：
①记甲快递公司的快递员的日工资为
（单位：元），求的分布列和数学期望；
②小赵拟到甲、乙两家快递公司中的一家应聘快递员的工作，如果仅从日收入的角度考虑，请你利用所学的统计学知识为他作出选择，并说明理由．
