Question

已知二面角α-AB-β的平面角是锐角θ，α内一点C到β的距离为3，点C到棱AB的距离为4，那么tanθ的值等于（　　）

• A、

  4

  5

• B、

  3

  5

• C、

  3

  7

  7

• D、

  1

  3

  7

Answer 1

分析：先作CE⊥AB，CD⊥β，连接ED，得到∠CED是二面角α-AB-β的平面角，在直角三角形CED中求出∠CED的正切值即可．

解答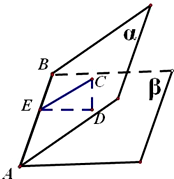：解：如图，作CE⊥AB，CD⊥β，连接ED，
由条件可知，∠CED=θ，CD=3，CE=4
∴ED=

7

，tanθ=

3

7

=

3 7

7

，
故选C

点评：本题主要考查了平面与平面之间的位置关系，考查空间想象能力、运算能力和推理论证能力，属于基础题．