题目内容
已知二面角α-AB-β为120°，AC?α，BD?β，且AC⊥AB，BD⊥AB，AB=AC=BD=a，则CD的长为分析：由题，在平面β中可过A作AB的垂线，过D作BD的垂线，两者交于E连接CE，可证得CE垂直于DE，在直角三角形EBC中用勾股定理求出CD的长度，得到答案
解答：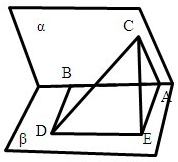
解：由题意，作出如图的图象，在平面β中可过A作AB的垂线，过D作BD的垂线，两者交于E连接CE，
由作图知，四边形ABDE是矩形，故有DE=AB=a，AE=BD=a，AE⊥AB
又AC⊥AB，易得AB⊥面ACE，即有CE⊥AB，进而得CE⊥DE
有二面角的平面角的定义知，∠CAE=120°
在△CAE中，由余弦定义可得CE2=a2+a2-2×a2×（-
）=3a2，故CE=
a
在直角三角形CED中，由勾股定理得CD2=DE2+CE2=a2+3a2=4a2，
可得CD的长为2a
故答案为：2a．
解：由题意，作出如图的图象，在平面β中可过A作AB的垂线，过D作BD的垂线，两者交于E连接CE，由作图知，四边形ABDE是矩形，故有DE=AB=a，AE=BD=a，AE⊥AB
又AC⊥AB，易得AB⊥面ACE，即有CE⊥AB，进而得CE⊥DE
有二面角的平面角的定义知，∠CAE=120°
在△CAE中，由余弦定义可得CE2=a2+a2-2×a2×（-
| 1 |
| 2 |
| 3 |
在直角三角形CED中，由勾股定理得CD2=DE2+CE2=a2+3a2=4a2，
可得CD的长为2a
故答案为：2a．
点评：本题考查与二面角的平面角及求法解题的关键是作出二面角的平面角，在三角形中求出二面角的大小，其作题步骤为：作角，证角，求角．
练习册系列答案
阅读快车系列答案
相关题目
已知二面角α-AB-β的平面角是锐角θ，α内一点C到β的距离为3，点C到棱AB的距离为4，那么tanθ的值等于（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，已知二面角α-AB-β的大小为120°，PC⊥α于C，PD⊥β于D，且PC=2，PD=3．