Question

已知二面角α-AB-β是直二面角，P为棱AB上一点，PQ、PR分别在平面α、β内，且∠QPB=∠RPB=45°，则∠QPR为（　　）

A．45°

B．60°

C．120°

D．150°

Answer 1

分析：在正方体中，又底面和侧面所成的直二面为模型，构造出满足条件的几何图形，根据正方体的几何特征，解三角形求出∠QPR可得答案．

解答：解：以正方体的模型，构造满足条件的几何图形如下图所示

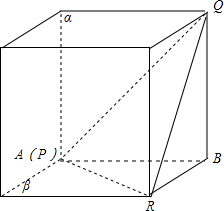
连接QR，由正方体的性质可得△PQR为等边三角形
故∠QPR=60°
故选B

点评：本题考查的知识点是空间直线与直线的夹角，其中又正方体为研究对象建立具体的模型，将线线夹角问题转化为解三角形问题是解答的关键．