题目内容
 如图,已知二面角α-AB-β的大小为120°,PC⊥α于C,PD⊥β于D,且PC=2,PD=3.
如图,已知二面角α-AB-β的大小为120°,PC⊥α于C,PD⊥β于D,且PC=2,PD=3.(1)求异面直线AB与CD所成角的大小;
(2)求点P到直线AB的距离.
分析:(1)根据题意,证出AB⊥平面PCD,从而得到AB⊥CD,即得异面直线AB与CD所成角的大小为90°.
(2)设平面ACD与直线AB交于点E,连结CE,DE,PE.证出∠CED为二面角α-AB-β的平面角,从而∠CED=120°.然后在四边形PCDE中利用余弦定理解三角形,算出CD=
,进而得到PE=
=
,得到P到直线AB的距离.
(2)设平面ACD与直线AB交于点E,连结CE,DE,PE.证出∠CED为二面角α-AB-β的平面角,从而∠CED=120°.然后在四边形PCDE中利用余弦定理解三角形,算出CD=
| 7 |
| CD |
| sin60° |
| 2 |
| 3 |
| 21 |
解答: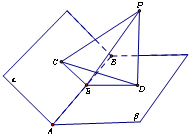 解:(1)∵PC⊥α于C,PD⊥β于D.
解:(1)∵PC⊥α于C,PD⊥β于D.
∴PC⊥AB,PD⊥AB.又PC∩PD=D.
∴AB⊥平面PCD.
∵CD?平面PCD,∴AB⊥CD,
即异面直线AB与CD所成角的大小为90°. …(6分)
(2)设平面ACD与直线AB交于点E,连结CE,DE,PE
由(1)可知,AB⊥平面PCD.
∴AB⊥CE,AB⊥DE,AB⊥PE.
∴∠CED为二面角α-AB-β的平面角,…(8分)
从而∠CED=120°.
∵PC⊥α,PD⊥β.∴PC⊥CE,PD⊥DE.
∴∠CPD=60°.又PC=2,PD=3.
∴由余弦定理,得CD2=4+9-12cos60°=7,从而CD=
.…(10分)
∵PE为四边形PCED的外接圆直径.
∴由正弦定理,得PE=
=
.
即点P到直线AB的距离等于
. …(12分)
 解:(1)∵PC⊥α于C,PD⊥β于D.
解:(1)∵PC⊥α于C,PD⊥β于D.∴PC⊥AB,PD⊥AB.又PC∩PD=D.
∴AB⊥平面PCD.
∵CD?平面PCD,∴AB⊥CD,
即异面直线AB与CD所成角的大小为90°. …(6分)
(2)设平面ACD与直线AB交于点E,连结CE,DE,PE
由(1)可知,AB⊥平面PCD.
∴AB⊥CE,AB⊥DE,AB⊥PE.
∴∠CED为二面角α-AB-β的平面角,…(8分)
从而∠CED=120°.
∵PC⊥α,PD⊥β.∴PC⊥CE,PD⊥DE.
∴∠CPD=60°.又PC=2,PD=3.
∴由余弦定理,得CD2=4+9-12cos60°=7,从而CD=
| 7 |
∵PE为四边形PCED的外接圆直径.
∴由正弦定理,得PE=
| CD |
| sin60° |
| 2 |
| 3 |
| 21 |
即点P到直线AB的距离等于
| 2 |
| 3 |
| 21 |
点评:本题在120度的二面角中,求异面直线所成角和点P到直线AB的距离,着重考查了线面垂直的判定与性质、二面角的平面角定义和正余弦定理等知识,属于中档题.

练习册系列答案
相关题目
 (2008•成都三模)如图,已知二面角α-PQ-β的大小为60°,点C为棱PQ一点,A∈β,AC=2,∠ACP=30°,则点A到平面α的距离为( )
(2008•成都三模)如图,已知二面角α-PQ-β的大小为60°,点C为棱PQ一点,A∈β,AC=2,∠ACP=30°,则点A到平面α的距离为( ) 如图,已知二面角α-l-β的平面角为45°,在半平面α内有一个半圆O,其直径AB在l上,M是这个半圆O上任一点(除A、B外),直线AM、BM与另一个半平面β所成的角分别为θ1、θ2.试证明cos2θ1+cos2θ2为定值.
如图,已知二面角α-l-β的平面角为45°,在半平面α内有一个半圆O,其直径AB在l上,M是这个半圆O上任一点(除A、B外),直线AM、BM与另一个半平面β所成的角分别为θ1、θ2.试证明cos2θ1+cos2θ2为定值.

 C.
C. D.
D.