Question

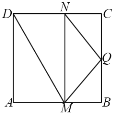
【题目】如图，在边长等于2正方形中，点Q是中点，点M，N分别在线段上移动（M不与A，B重合，N不与C，D重合），且，沿着将四边形折起，使得面面，则三棱锥体积的最大值为________；当三棱锥体积最大时，其外接球的表面积为________．

Answer 1

【答案】

【解析】

（1）依题意设设,则,利用椎体体积公式列式,再根据二次函数可得出最大值.

（2）依题意建立如图空间直角坐标系,列出各点的坐标,设球心坐标, 根据球心到各点距离等半径求球心坐标,即可得出半径,最后求出三棱锥的外接球面积.

依题意设,则,

因为,所以,又面面，面面，所以面，

所以是三棱锥的高，

所以三棱锥的体积，

当时，有最大值，

（2）由（1）知道三棱锥体积取得最大值时, ，

折起如图所示：依题意可建立如图所示空间直角坐标系：所以,,,，

设三棱锥外接球的球心为，

，

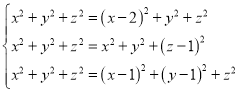解,所以，

外接球面积为.

故答案为：.