题目内容
11.已知数列{an}的前n项和Sn满足$\frac{1}{2}$Sn=an-1.(1)求数列{an}的通项公式;
(2)求证:数列{an}中的任意三项不可能成等差数列;
(3)设bn=$\frac{{a}_{n}}{({a}_{n}-1)^{2}}$,Tn为{bn}的前n项和,求证:Tn<3.
分析 (1)运用数列的通项和前n项和的关系,结合等比数列的通项公式,即可得到所求;
(2)运用反证法,假设数列{an}中的任意三项成等差数列,由(1)的结论,推出矛盾,即可得证;
(3)把数列的通项公式放大,然后利用等比数列的求和公式求和后再放大得答案.
解答 (1)解:n=1时,$\frac{1}{2}$S1=a1-1=$\frac{1}{2}$a1,
可得a1=2,
n>1时,$\frac{1}{2}$Sn-1=an-1-1,
与$\frac{1}{2}$Sn=an-1,
相减可得,$\frac{1}{2}$an=an-an-1,
即为an=2an-1,
即有数列{an}为等比数列,且an=2n;
(2)证明:假设数列{an}中的任意三项成等差数列,
由它们构成等比数列,则它们为公比为1的常数列,
这与公比为2的等比数列矛盾,故假设错误,
则数列{an}中的任意三项不可能成等差数列;
(3)证明:bn=$\frac{{a}_{n}}{({a}_{n}-1)^{2}}$=$\frac{{2}^{n}}{({2}^{n}-1)^{2}}$
=$\frac{{2}^{n}}{{2}^{2n}-2•{2}^{n}+1}$<$\frac{1}{{2}^{n-1}}$(n≥2),
∴Tn=b1+b2+…+bn<b1+$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n-1}})}{1-\frac{1}{2}}$
=2+1-$\frac{1}{{2}^{n-1}}$=3-$\frac{1}{{2}^{n-1}}$<3.
点评 本题考查了数列的通项和前n项和的关系,考查等比数列的通项和求和公式的运用,考查了反证法和放缩法证明数列不等式,是中档题.

练习册系列答案
相关题目
20.已知$\frac{1-tanα}{1+tanα}$=2,则tan(α+$\frac{π}{4}$)=( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
20.在极坐标系中,曲线C的方程为F(ρ,θ)=0,则F(ρ0,θ0)=0是点P(ρ0,θ0)在曲线C上的( )
| A. | 充要条件 | B. | 充分非必要条件 | ||
| C. | 必要非充分条件 | D. | 非充分非必要条件 |
1.若a>0,b>0,且a+b=2,则ab+$\frac{1}{ab}$的最小值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 2$\sqrt{2}$ |
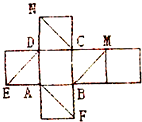 如图是正方体的平面展开图,在这个正方体中:
如图是正方体的平面展开图,在这个正方体中: