题目内容
 (2012•开封一模)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,PA=AB,G为PD的中点,E点在AB上,平面PEC⊥平面PDC.
(2012•开封一模)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,PA=AB,G为PD的中点,E点在AB上,平面PEC⊥平面PDC.(I)求证:AG∥平面PEC;
(Ⅱ)求面PEC与面PAD所成二面角的余弦值.
分析:(Ⅰ)因为平面PEC⊥平面PDC,过E作交线PC的垂线EF,得到EF⊥平面PCD,经证明可得AG⊥平面PCD,从而得到AG∥EF,
进一步说明线面平行;
(Ⅱ)以A为原点,AB、AD、AP所在直线分别为x、y、z轴建立空间直角坐标系,求出平面PAD的法向量,运用两个平面的法向量求二面角的大小.
进一步说明线面平行;
(Ⅱ)以A为原点,AB、AD、AP所在直线分别为x、y、z轴建立空间直角坐标系,求出平面PAD的法向量,运用两个平面的法向量求二面角的大小.
解答: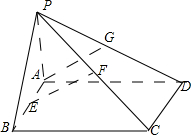 (Ⅰ)证明:∵CD⊥AD,CD⊥PA,PA∩AD=A,∴CD⊥平面PAD,∴CD⊥AG,又PD⊥AG,∴AG⊥平面PCD,
(Ⅰ)证明:∵CD⊥AD,CD⊥PA,PA∩AD=A,∴CD⊥平面PAD,∴CD⊥AG,又PD⊥AG,∴AG⊥平面PCD,
作EF⊥PC于F,因为平面PEC⊥面PCD,∴EF⊥平面PCD,
又由AG⊥平面PCD,∴EF∥AG,
∵AG在平面PCE外,EF在平面PEC内,
∴AG∥平面PEC.
(Ⅱ)解:由EF∥AG,FG∥AE,∴EG∥CD,即F是PC的中点,FG=
CD,即E为AB的中点,
建立如图所示的坐标系.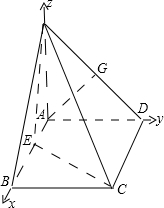
设
=(x1,y1,z1)是平面PEC的法向量,设AB=2,则E(1,0,0),C(2,2,0),D(0,2,0),P(0,0,2),
=(2,2,0),
=(1,2,0),
=(-1,0,2).
由
•
=(x1,y1,z1)(1,2,0)=x1+2y1=0①
•
=(x1,y1,z1)(-1,0,2)=-x1+2z1=0②
联立①②,取z1=1得:x1=2,y1=-1,z1=1,∴
=(2,-1,1).
设面PEC与面PAD所成二面角,∴cosθ=|
|=
,
所以所求的二面角的余弦值为
.
 (Ⅰ)证明:∵CD⊥AD,CD⊥PA,PA∩AD=A,∴CD⊥平面PAD,∴CD⊥AG,又PD⊥AG,∴AG⊥平面PCD,
(Ⅰ)证明:∵CD⊥AD,CD⊥PA,PA∩AD=A,∴CD⊥平面PAD,∴CD⊥AG,又PD⊥AG,∴AG⊥平面PCD,作EF⊥PC于F,因为平面PEC⊥面PCD,∴EF⊥平面PCD,
又由AG⊥平面PCD,∴EF∥AG,
∵AG在平面PCE外,EF在平面PEC内,
∴AG∥平面PEC.
(Ⅱ)解:由EF∥AG,FG∥AE,∴EG∥CD,即F是PC的中点,FG=
| 1 |
| 2 |
建立如图所示的坐标系.

设
| n |
| AC |
| EC |
| EP |
由
| n |
| EC |
| n |
| EP |
联立①②,取z1=1得:x1=2,y1=-1,z1=1,∴
| n |
设面PEC与面PAD所成二面角,∴cosθ=|
| ||||
|
|
| ||
| 3 |
所以所求的二面角的余弦值为
| ||
| 3 |
点评:本题考查了直线和平面平行的性质,考查了二面角的平面角,求二面角的平面角可以建立空间直角坐标系,求出两个平面的法向量
,
,然后借助于公式cosθ=
求解,求出θ后,注意分析θ是二面角的平面角还是其补角,此题是中档题.
| n1 |
| n2 |
| ||||
|
|

练习册系列答案
相关题目
 (2012•开封一模)一个几何体的三视图如图所示,已知这个几何体的体积为
(2012•开封一模)一个几何体的三视图如图所示,已知这个几何体的体积为 (2012•开封一模)函数f(x)满足f(0)=0,其导函数f′(x)的图象如图,则f(x)的图象与x轴所围成的封闭图形的面积为( )
(2012•开封一模)函数f(x)满足f(0)=0,其导函数f′(x)的图象如图,则f(x)的图象与x轴所围成的封闭图形的面积为( )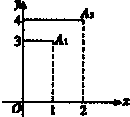 (2012•开封一模)
(2012•开封一模)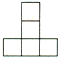 (2012•开封一模)用若干个体积为1的正方体搭成一个几何体,其正视图、侧视图都是如图所示的图形,则这个几何体的最小体积是( )
(2012•开封一模)用若干个体积为1的正方体搭成一个几何体,其正视图、侧视图都是如图所示的图形,则这个几何体的最小体积是( )