题目内容
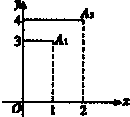 (2012•开封一模)(ax+1)n=anxn+an-1xn-1+…+a1x+a0(n∈N*),点列Ai(i,ai)(i=0,1,2,…n)的部分图象如图所示,则实数a的值为( )
(2012•开封一模)(ax+1)n=anxn+an-1xn-1+…+a1x+a0(n∈N*),点列Ai(i,ai)(i=0,1,2,…n)的部分图象如图所示,则实数a的值为( )分析:根据题意,结合图形可得a1=3,a2=4,再结合二项式定理可得a1、a2的值,即可得关于a、n的方程组,解可得a的值,即可得答案.
解答:解:根据题意,点A1的坐标为(1,3),点A2的坐标为(2,4),
则在(ax+1)n=anxn+an-1xn-1+…+a1x+a0(n∈N*)中,有a1=3,a2=4,
又由二项式定理可得a1=a•Cn1=na,a2=a2•Cn2=
a2,
则有na=3,
a2=4,
解可得a=
,n=3,
故选C.
则在(ax+1)n=anxn+an-1xn-1+…+a1x+a0(n∈N*)中,有a1=3,a2=4,
又由二项式定理可得a1=a•Cn1=na,a2=a2•Cn2=
| n(n-1) |
| 2 |
则有na=3,
| n(n-1) |
| 2 |
解可得a=
| 1 |
| 3 |
故选C.
点评:本题考查二项式定理的应用,注意正确理解题意,结合图形,分析得到a1、a2的值.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 (2012•开封一模)一个几何体的三视图如图所示,已知这个几何体的体积为
(2012•开封一模)一个几何体的三视图如图所示,已知这个几何体的体积为