题目内容
(12分)设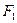 、
、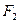 分别是椭圆
分别是椭圆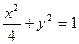 的左、右焦点.
的左、右焦点.
(Ⅰ)若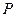 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求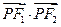 的最大值和最小值;
的最大值和最小值;
(Ⅱ)设过定点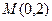 的直线
的直线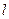 与椭圆交于不同的两点
与椭圆交于不同的两点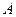 、
、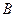 ,且∠
,且∠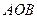 为钝角(其中
为钝角(其中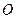 为坐标原点),求直线
为坐标原点),求直线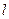 的斜率
的斜率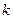 的取值范围.
的取值范围.
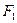 、
、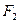 分别是椭圆
分别是椭圆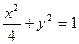 的左、右焦点.
的左、右焦点.(Ⅰ)若
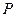 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求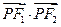 的最大值和最小值;
的最大值和最小值;(Ⅱ)设过定点
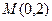 的直线
的直线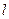 与椭圆交于不同的两点
与椭圆交于不同的两点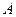 、
、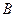 ,且∠
,且∠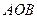 为钝角(其中
为钝角(其中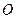 为坐标原点),求直线
为坐标原点),求直线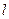 的斜率
的斜率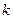 的取值范围.
的取值范围.(Ⅰ)易知 所以
所以 ,设
,设
则
 (2分)
(2分)
因为 ,故当
,故当 ,即点
,即点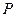 为椭圆短轴端点时,
为椭圆短轴端点时, 有最小值
有最小值
当 ,即点
,即点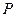 为椭圆长轴端点时,
为椭圆长轴端点时, 有最大值
有最大值 . (4分)
. (4分)
(Ⅱ)显然直线 不满足题设条件,可设直线
不满足题设条件,可设直线 ,
,
联立 ,消去
,消去 ,整理得:
,整理得:
∴ (6分)
(6分)
由 得:
得: ① (7分)
① (7分)
又
∴ (8分)
(8分)
又

 (10分)
(10分)
∵ ,即
,即 ② (11分)
② (11分)
故由①、②得 ∴
∴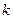 的取值范围是
的取值范围是 . (12分)
. (12分)
 所以
所以 ,设
,设
则

 (2分)
(2分)因为
 ,故当
,故当 ,即点
,即点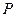 为椭圆短轴端点时,
为椭圆短轴端点时, 有最小值
有最小值
当
 ,即点
,即点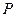 为椭圆长轴端点时,
为椭圆长轴端点时, 有最大值
有最大值 . (4分)
. (4分)(Ⅱ)显然直线
 不满足题设条件,可设直线
不满足题设条件,可设直线 ,
,联立
 ,消去
,消去 ,整理得:
,整理得:
∴
 (6分)
(6分)由
 得:
得: ① (7分)
① (7分)又

∴
 (8分)
(8分)又


 (10分)
(10分)∵
 ,即
,即 ② (11分)
② (11分)故由①、②得
 ∴
∴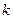 的取值范围是
的取值范围是 . (12分)
. (12分)略

练习册系列答案
相关题目
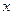 轴上,离心率为
轴上,离心率为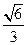 ,两条准线间的距离为6. 椭圆W的左焦点为
,两条准线间的距离为6. 椭圆W的左焦点为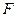 ,过左准线与
,过左准线与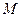 任作一条斜率不为零的直线
任作一条斜率不为零的直线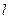 与椭圆W交于不同的两点
与椭圆W交于不同的两点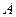 、
、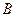 ,点
,点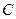 .
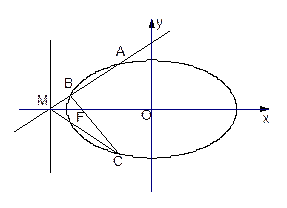
.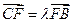 (
(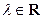 );
);
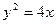 以F2为焦点,点P为抛物线和椭圆的一个交点,若PF2与x轴成45°,则e的值为 ▲ .
以F2为焦点,点P为抛物线和椭圆的一个交点,若PF2与x轴成45°,则e的值为 ▲ .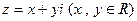 与复平面上点
与复平面上点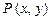 对应.
对应. 满足条件
满足条件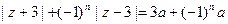 (其中
(其中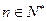 ,常数
,常数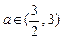 ),当
),当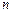 为奇数时,动点
为奇数时,动点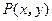 的轨迹为
的轨迹为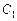 ;当
;当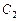 ,且两条曲线都经过点
,且两条曲线都经过点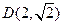 ,求轨迹
,求轨迹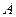 ,使点
,使点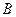
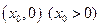 的最小距离不小于
的最小距离不小于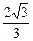 ,求实数
,求实数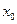 的取值范围.
的取值范围.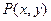 是椭圆
是椭圆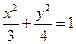 上的动点。
上的动点。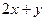 的取值范围
的取值范围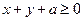 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。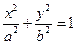 的左焦点
的左焦点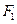 ,右顶点A,上顶点B,且
,右顶点A,上顶点B,且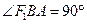 ,则椭圆的离心率是
,则椭圆的离心率是



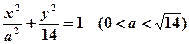 的两焦点为
的两焦点为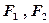 ,现将坐标平面沿
,现将坐标平面沿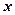 轴折成二面角,二面角的度数为
轴折成二面角,二面角的度数为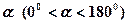 ,已知折起后两焦点的距离
,已知折起后两焦点的距离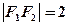 ,则满足题设的一组数值:
,则满足题设的一组数值:
 (只需写出一组就可以,不必写出所有情况)
(只需写出一组就可以,不必写出所有情况)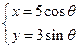 (
( 为参数),则它的离心率为 .
为参数),则它的离心率为 .  的长轴长为
的长轴长为