题目内容
已知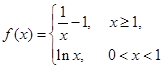 ,若
,若 恒成立,则
恒成立,则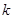 的取值范围是( )
的取值范围是( )
A.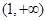 | B.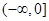 | C.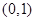 | D. |
D
解析试题分析: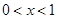 时,函数
时,函数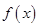 在
在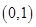 上是增函数,且
上是增函数,且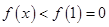 ;当
;当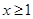 时,函数
时,函数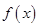 在
在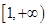 上单调递减,且
上单调递减,且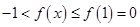 。令
。令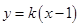 ,表示过定点
,表示过定点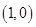 斜率为
斜率为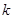 的直线。当
的直线。当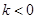 时,直线必与函数
时,直线必与函数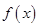 有两个交点,不能使
有两个交点,不能使 恒成立。当
恒成立。当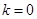 时,显然
时,显然 恒成立;当
恒成立;当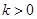 时,直线与函数
时,直线与函数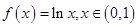 相切时,因定点
相切时,因定点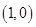 即在直线
即在直线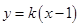 上又在函数
上又在函数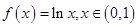 图像上,则此点
图像上,则此点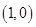 即为切点,因为
即为切点,因为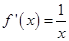 ,由导数的几何意义可得
,由导数的几何意义可得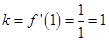 ,有数形结合分析可知
,有数形结合分析可知 时
时 恒成立;显然当
恒成立;显然当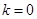 时
时 也恒成立。综上可得
也恒成立。综上可得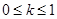 。故D正确。
。故D正确。
考点:1函数的单调性;2数形结合思想。

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
设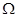 为平面直角坐标系
为平面直角坐标系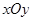 中的点集,从
中的点集,从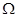 中的任意一点
中的任意一点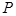 作
作 轴、
轴、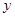 轴的垂线,垂足分别为
轴的垂线,垂足分别为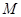 ,
, ,记点
,记点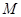 的横坐标的最大值与最小值之差为
的横坐标的最大值与最小值之差为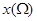 ,点
,点 的纵坐标的最大值与最小值之差为
的纵坐标的最大值与最小值之差为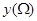 . 若
. 若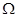 是边长为1的正方形,给出下列三个结论:
是边长为1的正方形,给出下列三个结论:
①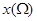 的最大值为
的最大值为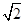 ;
;
②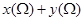 的取值范围是
的取值范围是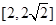 ;
;
③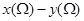 恒等于0.其中所有正确结论的序号是( )
恒等于0.其中所有正确结论的序号是( )
| A.① | B.②③ | C.①② | D.①②③ |
已知函数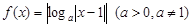 ,若
,若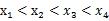 ,
,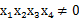
且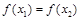
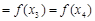 ,则
,则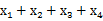 =( )
=( )
| A.2 | B.4 | C.8 | D.随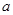 值变化 值变化 |
偶函数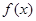 满足
满足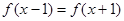 ,且在
,且在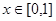 时,
时,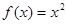 ,则关于
,则关于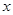 的方程
的方程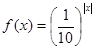 在
在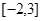 上的根的个数是
上的根的个数是
| A.3 | B.4 | C.5 | D.6 |
已知函数y=ax2+bx+c(a≠0)的图象经过(-1,3)和(1,1)两点,若0<c<1,则a的取值范围是 ( )
| A.(1,3) | B.(1,2) |
| C.[2,3) | D.[1,3] |
下列函数为偶函数的是
| A.y=sinx | B.y=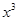 | C.y=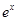 | D.y=ln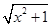 |
设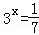 ,则( )
,则( )
| A.﹣2<x<﹣1 | B.﹣3<x<﹣2 |
| C.﹣1<x<0 | D.0<x<1 |
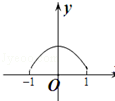
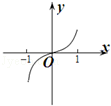
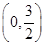 时,f(x)=ln(x2-x+1),则函数f(x)在区间[0,6]上的零点个数为( )
时,f(x)=ln(x2-x+1),则函数f(x)在区间[0,6]上的零点个数为( )