题目内容
已知△ABC的三边长分别为a、b、c,且满足abc=![]()
(1)是否存在边长均为整数的△ABC?若存在,求出三边长;若不存在,说明理由。
(2)若a>1,b>1,c>1,求出△ABC周长的最小值。
(1)存在三边长均为整数的△ABC,其三边长分别为4,5,6或3,7,8,(2)△ABC的周长最小值为![]() ,当且仅当
,当且仅当![]() 时,取得此最小值
时,取得此最小值
解析:
(1)不妨设整数a≥b≥c,显然c≥2。
若c≥5,这时![]()
由![]() ,可得
,可得
![]() 。
。
矛盾。
故c只可能取2,3,4。
当c=2时,![]() ,有
,有![]()
又a≥b≥2,故无解。
当c=3时,![]() ,即
,即![]()
又a≥b≥3,故
![]() 或
或![]() 或
或![]()
解得![]() 或
或![]() 或
或![]()
能构成三角形的只有a=8,b=7,c=3。
当c=4时,同理解得a=9,b=4或a=6,b=5。
能构成三角形的只有a=6,b=5,c=4。
故存在三边长均为整数的△ABC,其三边长分别为4,5,6或3,7,8
(2)由![]() ,可得
,可得
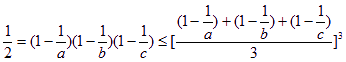
所以,![]()
又![]() ,则有
,则有
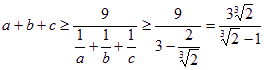
故△ABC的周长最小值为![]() ,当且仅当
,当且仅当![]() 时,取得此最小值。
时,取得此最小值。

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
已知△ABC的三边长为a、b、c,满足直线ax+by+c=0与圆x2+y2=1相离,则△ABC是( )
| A、锐角三角形 | B、直角三角形 | C、钝角三角形 | D、以上情况都有可能 |