题目内容
已知三个函数模型：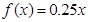
，
，
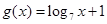，当
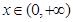，随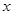
的增大，三个函数中的增长速度越来越快的是（ ）
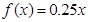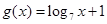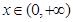，，，当，随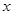的增大，三个函数中的增长速度越来越快的是（ ）A． | B． | C． | D． |
C
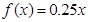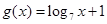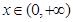解：因为三个函数模型：，，，当中，指数函数是爆炸型增长，因此选C.
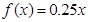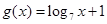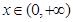，，，当中，指数函数是爆炸型增长，因此选C.
练习册系列答案
相关题目
题目内容
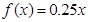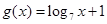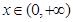，，，当，随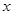的增大，三个函数中的增长速度越来越快的是（ ）| A． | B． | C． | D． |
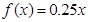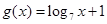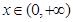，，，当中，指数函数是爆炸型增长，因此选C.
米，宽
米的长方形体育馆．按照建筑要求，每隔
米（
，
为正常数）需打建一个桩位，每个桩位需花费
万元（桩位视为一点且打在长方形的边上），桩位之间的
万元，在不计地板和天花板的情况下，当
与时间
的关系，可近似地表示为
。只有当河流中碱的浓度不低于1时，才能对污染产生有效的抑制作用。
的定义域为
，部分对应值如下表，
，则
的取值范围为 ▲ ．
在 
上为奇函数，且
上为增函数，
,则不等式
的解集为 _______.
是定义在正整数集上的函数,且
成立时，总可推出
成立”，那么，下列命题总成立的是（ ）
成立，则
成立
成立，则当
时，均有
成立，则
成立 
成立，则当
时，均有
，若
，则
，则
的表达式为（ ）
