题目内容
已知正数数列{an}中,a1=2.若关于x的方程x2-(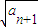 )x+
)x+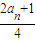 =0(n∈N×))对任意自然数n都有相等的实根.
=0(n∈N×))对任意自然数n都有相等的实根.(1)求a2,a3的值;
(2)求证
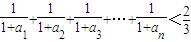 (n∈N×).
(n∈N×).
【答案】分析:(1)由题意得△=an+1-2n-1=0,可得a2=5,a3=11.
(2)由于an+1=2an+1,所以数列an+1是以a1+1=3为首项,公比为2的等比数列,知数列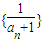 是以
是以 为首项,公比为
为首项,公比为 的等比数列,于是可以证明
的等比数列,于是可以证明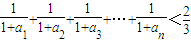 .
.
解答:解:(1)由题意得△=an+1-2n-1=0,即an+1=2an+1,进而可得a2=5,a3=11.
(2)由于an+1=2an+1,所以an+1=2(an+1),因为a1+1=3≠0,所以数列an+1是以a1+1=3为首项,公比为2的等比数列,知数列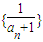 是以
是以 为首项,公比为
为首项,公比为 的等比数列,于是
的等比数列,于是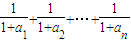 =
=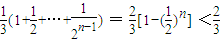 .
.
点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答.
(2)由于an+1=2an+1,所以数列an+1是以a1+1=3为首项,公比为2的等比数列,知数列
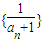 是以
是以 为首项,公比为
为首项,公比为 的等比数列,于是可以证明
的等比数列,于是可以证明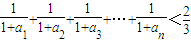 .
.解答:解:(1)由题意得△=an+1-2n-1=0,即an+1=2an+1,进而可得a2=5,a3=11.
(2)由于an+1=2an+1,所以an+1=2(an+1),因为a1+1=3≠0,所以数列an+1是以a1+1=3为首项,公比为2的等比数列,知数列
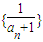 是以
是以 为首项,公比为
为首项,公比为 的等比数列,于是
的等比数列,于是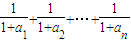 =
=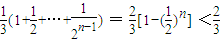 .
.点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答.

练习册系列答案
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目