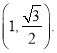题目内容
【题目】在平面直角坐标系xOy中,已知圆C:x2+y2=4和直线l:x=4,M为l上一动点,A1 , A2为圆C与x轴的两个交点,直线MA1 , MA2与圆C的另一个交点分别为P、Q.
(1)若M点的坐标为(4,2),求直线PQ方程;
(2)求证直线PQ过定点,并求出此定点的坐标.
【答案】
(1)解:当M(4,2),
则A1(﹣2,0),A2(2,0).
直线MA1的方程:x﹣3y+2=0,
解 ![]() 得
得 ![]() .
.
直线MA2的方程:x﹣y﹣2=0,
解 ![]() 得Q(0,﹣2),
得Q(0,﹣2),
由两点式可得直线PQ的方程为2x﹣y﹣2=0
(2)证明:设M(4,t),则直线MA1的方程: ![]() ,直线MA2的方程:
,直线MA2的方程: ![]()
由 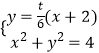 得
得 ![]()
由 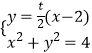 得
得 ![]()
当 ![]() 时,
时, ![]() ,
,
则直线PQ: ![]()
化简得 ![]() ,恒过定点(1,0)
,恒过定点(1,0)
当 ![]() 时,
时, ![]() ,直线PQ:x=1,恒过定点(1,0)
,直线PQ:x=1,恒过定点(1,0)
故直线PQ过定点(1,0)
【解析】(1)求出A1 , A2的坐标,可求直线MA1的方程、直线MA2的方程,与圆的方程联立,求出P,Q的坐标,由两点式求直线PQ方程;(2)设M(4,t),则直线MA1的方程: ![]() ,直线MA2的方程:
,直线MA2的方程: ![]() ,分别代入圆的方程,求出P,Q的坐标,分类讨论,确定直线PQ的方程,即可得出结论.
,分别代入圆的方程,求出P,Q的坐标,分类讨论,确定直线PQ的方程,即可得出结论.

练习册系列答案
相关题目