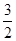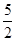题目内容
抛物线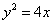 的焦点为F,点
的焦点为F,点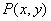 为该抛物线上的动点,又点
为该抛物线上的动点,又点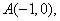 则
则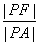 的最小值是
的最小值是
A.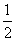 | B.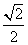 | C.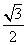 | D.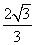 |
B ;
解析试题分析:如图,自点P向抛物线的准线作垂线,垂足为B,由抛物线的定义可知,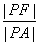 即为
即为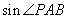 ,
,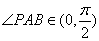 ,由正弦函数的单调性及点P在抛物线上移动的情况,可知,当
,由正弦函数的单调性及点P在抛物线上移动的情况,可知,当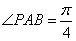 时,
时,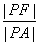 取到最小值
取到最小值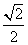 ,选B。
,选B。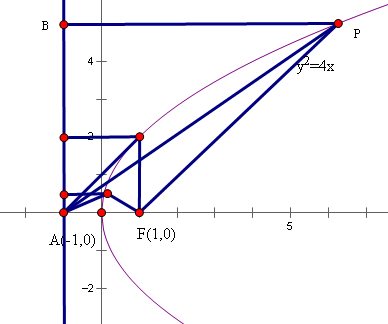
考点:本题主要考查抛物线的定义、几何性质,正弦函数的单调性。
点评:简单题,利用数形结合思想,将比值转化成求角的正弦,利用正弦函数的单调性即得。

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
已知 满足
满足 ,记目标函数
,记目标函数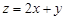 的最大值为7,最小值为1,则
的最大值为7,最小值为1,则 ( )
( )
| A.2 | B.1 | C.-1 | D.-2 |
直线 与抛物线
与抛物线 所围成的图形面积是( )
所围成的图形面积是( )
| A.20 | B. | C. | D. |
若点O和点F分别为双曲线 的中心和左焦点,点P为双曲线右支上的任意一点,则
的中心和左焦点,点P为双曲线右支上的任意一点,则 的最小值为( )
的最小值为( )
| A.-6 | B.-2 | C.0 | D.10 |
抛物线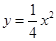 的焦点坐标是( )
的焦点坐标是( )
A.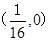 | B.(1,0) | C.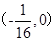 | D.(0,1) |
已知曲线C:y=2x2,点A(0,-2)及点B(3,a),从点A观察点B,要实现不被曲线C挡住,则实数a的取值范围是( )
| A.(4,+∞) | B.(-∞,4) |
| C.(10,+∞) | D.(-∞,10) |
双曲线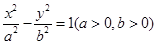 与直线
与直线 有公共点,则双曲线的离心率的取值范围是( )
有公共点,则双曲线的离心率的取值范围是( )
A.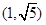 | B.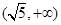 | C.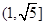 | D.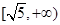 |
若抛物线顶点为坐标原点,对称轴为x轴,焦点在3x-4y-12=0上,那么抛物线方程是( )
A.y =16x =16x | B.y =-16x =-16x | C.y =12x =12x | D.y =-12x =-12x |
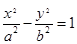 (
( )的两个焦点,若F1、F2、P(0,2
)的两个焦点,若F1、F2、P(0,2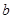 )是正三角形的三个顶点,则双曲线离心率是( )
)是正三角形的三个顶点,则双曲线离心率是( )