Question

【题目】已知函数f（x）= + ．
（1）求函数f（x）的定义域和值域；
（2）设F（x）= [f2（x）﹣2]+f（x）（a为实数），求F（x）在a＜0时的最大值g（a）；
（3）对（2）中g（a），若﹣m2+2tm+ ≤g（a）对a＜0所有的实数a及t∈[﹣1，1]恒成立，求实数m的取值范围．

Answer 1

【答案】
（1）解：由1+x≥0且1﹣x≥0，得﹣1≤x≤1，

所以函数的定义域为[﹣1，1]，

又[f（x）]2=2+2 ∈[2，4]，由f（x）≥0，得f（x）∈[ ，2]，

所以函数值域为[ ，2]

（2）解：因为F（x）= =a + + ，

令t=f（x）= + ，则 = ﹣1，

∴F（x）=m（t）=a（ ﹣1）+t= ，t∈[ ，2]，

由题意知g（a）即为函数m（t）= ，t∈[ ，2]的最大值．

注意到直线t=﹣ 是抛物线m（t）= 的对称轴．

因为a＜0时，函数y=m（t），t∈[ ，2]的图象是开口向下的抛物线的一段，

①若t=﹣ ∈（0， ]，即a≤﹣ ，则g（a）=m（ ）= ；

②若t=﹣ ∈（ ，2]，即﹣ ＜a≤﹣ ，则g（a）=m（﹣ ）=﹣a﹣ ；

③若t=﹣ ∈（2，+∞），即﹣ ＜a＜0，则g（a）=m（2）=a+2，

综上有g（a）=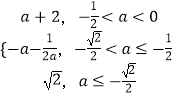

（3）解：易得 ，

由﹣ ≤g（a）对a＜0恒成立，即要使﹣ ≤gmin（a）= 恒成立，

m2﹣2tm≥0，令h（t）=﹣2mt+m2，对所有的t∈[﹣1，1]，h（t）≥0成立，

只需 ，

解得m的取值范围是m≤﹣2或m=0，或m≥2

【解析】（1）由1+x≥0且1﹣x≥0可求得定义域，先求[f（x）]2的值域，再求f（x）的值域；（2）F（x）=a + + ，令t=f（x）= + ，则 = ﹣1，由此可转化为关于t的二次函数，按照对称轴t=﹣ 与t的范围[ ，2]的位置关系分三种情况讨论，借助单调性即可求得其最大值；（3）先由（2）求出函数g（x）的最小值，﹣ ≤g（a）对a＜0恒成立，即要使﹣ ≤gmin（a）恒成立，从而转化为关于t的一次不等式，再根据一次函数的单调性可得不等式组，解出即可．