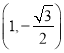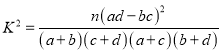题目内容
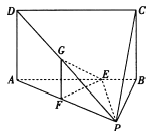
【题目】如图,正方形![]() 与梯形
与梯形![]() 所在的平面互相垂直,
所在的平面互相垂直,![]() ,
,![]() ∥
∥![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上.
上.

(I)当点![]() 为
为![]() 中点时,求证:
中点时,求证:![]() ∥平面
∥平面![]() ;
;
(II)当平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() 时,求三棱锥
时,求三棱锥![]() 的体积.
的体积.
【答案】(I)建立空间直角坐标系,证明![]() ,进而得证;(II)
,进而得证;(II)![]()
【解析】
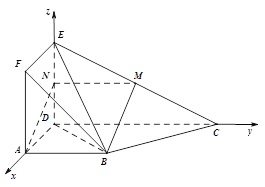
试题(1)要证明直线和平面平行,只需在平面内找一条直线,与平面外的直线平行即可,取![]() 中点
中点![]() ,连结
,连结![]() .可证明四边形
.可证明四边形![]() 为平行四边形. 于是,
为平行四边形. 于是,![]() ∥
∥![]() ,从而证明
,从而证明![]() 面
面![]() ;(2)要证明平面和平面垂直,只需在一个平面内找另一个平面的一条垂线,由面
;(2)要证明平面和平面垂直,只需在一个平面内找另一个平面的一条垂线,由面![]()
![]() 平面
平面![]() 且
且![]() ,可证
,可证![]() 平面
平面![]() ,从而
,从而![]() ,又可证
,又可证![]() ,故
,故![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ;(3)建立空间直角坐标系,设点M的坐标,求两个半平面的法向量,然后利用已知二面角的余弦值列方程,从而确定点M的位置,进而求三棱锥
;(3)建立空间直角坐标系,设点M的坐标,求两个半平面的法向量,然后利用已知二面角的余弦值列方程,从而确定点M的位置,进而求三棱锥![]() 的体积.
的体积.

试题解析:(1)证明 取![]() 中点
中点![]() ,连结
,连结![]() .在△
.在△![]() 中,
中,![]() 分别为
分别为![]() 的中点,
的中点,
则![]() ∥
∥![]() ,且
,且![]() .由已知
.由已知![]() ∥
∥![]() ,
,![]() ,因此,
,因此,![]() ∥
∥![]() ,且
,且![]() .所以,四边形
.所以,四边形![]() 为平行四边形. 于是,
为平行四边形. 于是,![]() ∥
∥![]() .又因为
.又因为![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,
,
所以![]() ∥平面
∥平面![]() ,从而可证.
,从而可证.
(2)证明 在正方形![]() 中,
中,![]() .又平面
.又平面![]()
![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,知
,知![]() 平面
平面![]() .所以
.所以![]() .在直角梯形
.在直角梯形![]() 中,
中,![]() ,
,![]() ,算得
,算得![]() .在△
.在△![]() 中,
中,![]() ,可得
,可得![]() .故
.故![]() 平面
平面![]() .又因为
.又因为![]() 平面
平面![]() ,所以,平面
,所以,平面![]() 平面
平面![]() .
.
(3)按如图建立空间直角坐标系,点![]() 与坐标原点
与坐标原点![]() 重合.设
重合.设![]() ,则
,则![]() ,又
,又![]() ,设
,设![]() ,则
,则![]() ,即
,即![]() .
.
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则![]() ,
,![]() .
.
取![]() ,得
,得![]() ,即得平面
,即得平面![]() 的一个法向量为
的一个法向量为![]() . 由题可知,
. 由题可知,![]() 是平面
是平面![]() 的一个法向量.因此,
的一个法向量.因此, ,即点
,即点![]() 为
为![]() 中点.此时,
中点.此时,![]() ,
,![]() 为三棱锥
为三棱锥![]() 的高,所以,
的高,所以,![]()
![]() .
.

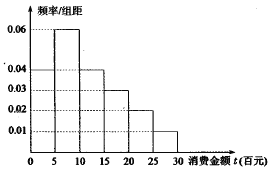
【题目】哈三中群力校区高二、六班同学用随机抽样的办法对所在校区老师的饮食习惯进行了一次调查, 饮食指数结果用茎叶图表示如图, 图中饮食指数低于70的人是饮食以蔬菜为主;饮食指数高于70的人是饮食以肉类为主.

(1)完成下列2×2列联表:

能否有99%的把握认为老师的饮食习惯与年龄有关?
(2)从群力校区任选一名老师, 设“选到45岁以上老师”为事件![]() , “饮食指数高于70的老师”为事件
, “饮食指数高于70的老师”为事件![]() , 用调查的结果估计
, 用调查的结果估计![]() 及
及![]() (用最简分数作答);
(用最简分数作答);
(3)为了给食堂提供老师的饮食信息, 根据(1)(2)的结论,能否有更好的抽样方法来估计老师的饮食习惯, 并说明理由.附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]()
【题目】某班甲、乙两名同学参加l00米达标训练,在相同条件下两人10次训练的成绩(单位:秒)如下:
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
甲 | 11.6 | 12.2 | 13.2 | 13.9 | 14.0 | 11.5 | 13.1 | 14.5 | 11.7 | 14.3 |
乙 | 12.3 | 13.3 | 14.3 | 11.7 | 12.0 | 12.8 | 13.2 | 13.8 | 14.1 | 12.5 |
(I)请作出样本数据的茎叶图;如果从甲、乙两名同学中选一名参加学校的100米比赛,从成绩的稳定性方面考虑,选派谁参加比赛更好,并说明理由(不用计算,可通过统计图直接回答结论).
(Ⅱ)从甲、乙两人的10次训练成绩中各随机抽取一次,求抽取的成绩中至少有一个比12.8秒差的概率.
(Ⅲ)经过对甲、乙两位同学的多次成绩的统计,甲、乙的成绩都均匀分布在![]() 之间,现甲、乙比赛一次,求甲、乙成绩之差的绝对值小于
之间,现甲、乙比赛一次,求甲、乙成绩之差的绝对值小于![]() 秒的概率.
秒的概率.