题目内容
【题目】已知f(x)=|x2-4x+3|.
(1)作出函数f(x)的图象;
(2)求函数f(x)的单调区间,并指出其单调性;
(3)求集合M={m|使方程f(x)=m有四个不相等的实根}.
【答案】(1)见解析.
(2)见解析.
(3) M={m|0<m<1}.
【解析】
(1)借助对称性作f(x)=|x2﹣4x+3|的图象即可,
(2)由图象写出函数f(x)的单调区间即可;
(3)作f(x)=|x2﹣4x+3|与y=m的图象,由二者的交点个数确定出集合M.
(1)当x2-4x+3≥0时,x≤1或x≥3,
∴f(x)=![]()
∴f(x)的图象为:
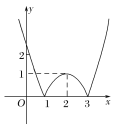
(2)由函数的图象可知f(x)的单调区间是(-∞,1],(2,3),(1,2],[3,+∞),其中(-∞,1],(2,3)是减区间;(1,2],[3,+∞)是增区间.
(3)由f(x)的图象知,当0<m<1时,f(x)=m有四个不相等的实根,所以M={m|0<m<1}.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
【题目】为了了解某省各景区在大众中的熟知度,随机从本省![]() 岁的人群中抽取了
岁的人群中抽取了![]() 人,得到各年龄段人数的频率分布直方图如图所示,现让他们回答问题“该省有哪几个国家
人,得到各年龄段人数的频率分布直方图如图所示,现让他们回答问题“该省有哪几个国家![]() 级旅游景区?”,统计结果如下表所示:
级旅游景区?”,统计结果如下表所示:
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
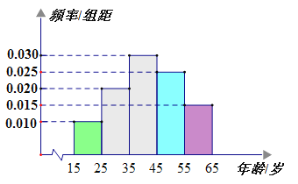
(1)分别求出![]() 的值;
的值;
(2)从第![]() 组回答正确的人中用分层抽样的方法抽取
组回答正确的人中用分层抽样的方法抽取![]() 人,求第
人,求第![]() 组每组抽取的人数;
组每组抽取的人数;
(3)在(2)中抽取的![]() 人中随机抽取
人中随机抽取![]() 人,求所抽取的人中恰好没有年龄段在
人,求所抽取的人中恰好没有年龄段在![]() 的概率
的概率


