题目内容
已知数列{an}满足a1=1,an>0,Sn是数列{an}的前n项和,对任意的n∈N*,有2Sn=p(2a2n+an-1),p为常数。
(1)求数列{an}的通项公式;
(2)记 ,求数列{bn}的前n项和Tn。
,求数列{bn}的前n项和Tn。
(1)求数列{an}的通项公式;
(2)记
 ,求数列{bn}的前n项和Tn。
,求数列{bn}的前n项和Tn。解:(1)当n=1时
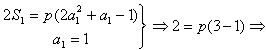 p=1
p=1
∴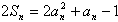
又
两式相减得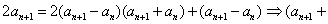
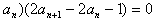
∵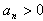
∴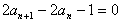
∴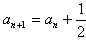
∴{an}是以1为首项,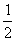 为公差的等差数列
为公差的等差数列
∴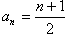 。
。
(2)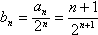
则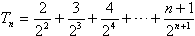
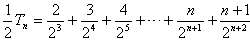
相减得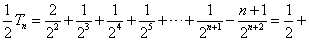
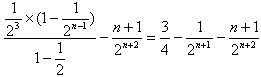
所以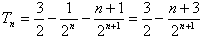 。
。
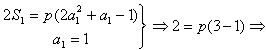 p=1
p=1∴
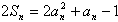
又

两式相减得
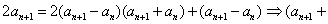
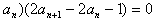
∵
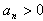
∴
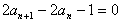
∴
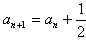
∴{an}是以1为首项,
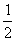 为公差的等差数列
为公差的等差数列∴
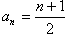 。
。(2)
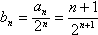
则
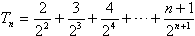
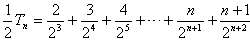
相减得
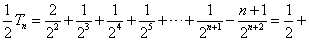
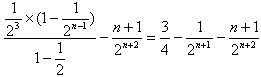
所以
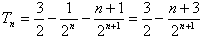 。
。
练习册系列答案
相关题目