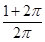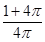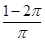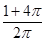题目内容
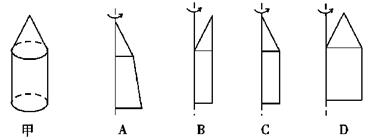
一个几何体的三视图如图3所示，其中主视图中
是边长为
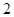的正三角形，俯视图为正六边形，那么该几何体的左视图的面积为 
A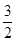． | B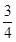． | C．1 | D． |
A
解析试题分析：有三视图可知该几何体是正六棱锥，底面正六边形边长为1侧棱长为2，棱锥高为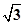
，左视图三角形底面边长为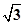，所以面积为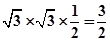
考点：几何体三视图
点评：先由三视图还原直观图，再在直观图中找到相应长度计算
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
已知某几何体的三视图如图所示，若该几何体的体积为24，则该几何体的底面积是（ ）
| A．6 | B．12 | C．18 | D．24 |
右图为某平面图形用斜二测画法画出的直观图，则其原来平面图形的面积是（ ）
| A．4 | B．4 | C．2 | D．8 |
半径为15 cm，圆心角为216°的扇形围成圆锥的侧面，则圆锥的高是( )
| A．14 cm | B．12 cm | C．10 cm | D．8 cm |
已知球的半径为2，相互垂直的两个平面分别截球面得两个圆．若两圆的公共弦长为2，则两圆的圆心距等于（ ）
| A．1 | B． | C． | D．2 |
将边长为1的正方形ABCD，沿对角线AC折起，使BD=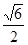
.则三棱锥D-ABC的体积为( )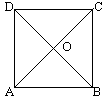
A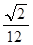． | B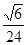． | C． | D． |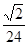
